library(tidyverse) # Sine Qua Non package in R
library(mosaic) # Our Favourite Bag of Tricks
library(ggformula) # Graphing
library(skimr) # Data Inspection and Summary
##
library(crosstable) # Fast stats for multiple variables in table form
library(tinytable) # Elegant Tables for our data
library(visdat) # Mapping missing data
library(naniar) # Missing data visualization and munging
library(janitor) # Clean the data
library(tinytable) # Printing Tables for our data
library(DT) # Interactive Tables for our data
library(ggrepel) # Repel overlapping text labels in ggplot2
library(marquee) # Annotations for ggplot2
How much of this and that?
2022-11-15
“The fear of death follows from the fear of life. A man who lives fully is prepared to die at any time.”
— Mark Twain
Plot Fonts and Theme
Code
library(systemfonts)
library(showtext)
## Clean the slate
systemfonts::clear_local_fonts()
systemfonts::clear_registry()
##
showtext_opts(dpi = 96) # set DPI for showtext
sysfonts::font_add(
family = "Alegreya",
regular = "../../../../../../fonts/Alegreya-Regular.ttf",
bold = "../../../../../../fonts/Alegreya-Bold.ttf",
italic = "../../../../../../fonts/Alegreya-Italic.ttf",
bolditalic = "../../../../../../fonts/Alegreya-BoldItalic.ttf"
)
sysfonts::font_add(
family = "Roboto Condensed",
regular = "../../../../../../fonts/RobotoCondensed-Regular.ttf",
bold = "../../../../../../fonts/RobotoCondensed-Bold.ttf",
italic = "../../../../../../fonts/RobotoCondensed-Italic.ttf",
bolditalic = "../../../../../../fonts/RobotoCondensed-BoldItalic.ttf"
)
showtext_auto(enable = TRUE) # enable showtext
##
theme_custom <- function() {
theme_bw(base_size = 10) +
# theme(panel.widths = unit(11, "cm"),
# panel.heights = unit(6.79, "cm")) + # Golden Ratio
theme(
plot.margin = margin_auto(t = 1, r = 2, b = 1, l = 1, unit = "cm"),
plot.background = element_rect(
fill = "bisque",
colour = "black",
linewidth = 1
)
) +
theme_sub_axis(
title = element_text(
family = "Roboto Condensed",
size = 10
),
text = element_text(
family = "Roboto Condensed",
size = 8
)
) +
theme_sub_legend(
text = element_text(
family = "Roboto Condensed",
size = 6
),
title = element_text(
family = "Alegreya",
size = 8
)
) +
theme_sub_plot(
title = element_text(
family = "Alegreya",
size = 14, face = "bold"
),
title.position = "plot",
subtitle = element_text(
family = "Alegreya",
size = 10
),
caption = element_text(
family = "Alegreya",
size = 6
),
caption.position = "plot"
)
}
## Use available fonts in ggplot text geoms too!
ggplot2::update_geom_defaults(geom = "text", new = list(
family = "Roboto Condensed",
face = "plain",
size = 3.5,
color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "label", new = list(
family = "Roboto Condensed",
face = "plain",
size = 3.5,
color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "marquee", new = list(
family = "Roboto Condensed",
face = "plain",
size = 3.5,
color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "text_repel", new = list(
family = "Roboto Condensed",
face = "plain",
size = 3.5,
color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "label_repel", new = list(
family = "Roboto Condensed",
face = "plain",
size = 3.5,
color = "#2b2b2b"
))
## Set the theme
ggplot2::theme_set(new = theme_custom())
## tinytable options
options("tinytable_tt_digits" = 2)
options("tinytable_format_num_fmt" = "significant_cell")
options(tinytable_html_mathjax = TRUE)
## Set defaults for flextable
flextable::set_flextable_defaults(font.family = "Roboto Condensed")
| Variable #1 | Variable #2 | Chart Names | Chart Shape | |
|---|---|---|---|---|
| Quant | None | Histogram |
| No | Pronoun | Answer | Variable/Scale | Example | What Operations? |
|---|---|---|---|---|---|
| 1 | How Many / Much / Heavy? Few? Seldom? Often? When? | Quantities, with Scale and a Zero Value.Differences and Ratios /Products are meaningful. | Quantitative/Ratio | Length,Height,Temperature in Kelvin,Activity,Dose Amount,Reaction Rate,Flow Rate,Concentration,Pulse,Survival Rate | Correlation |
What does this Chart tell us?
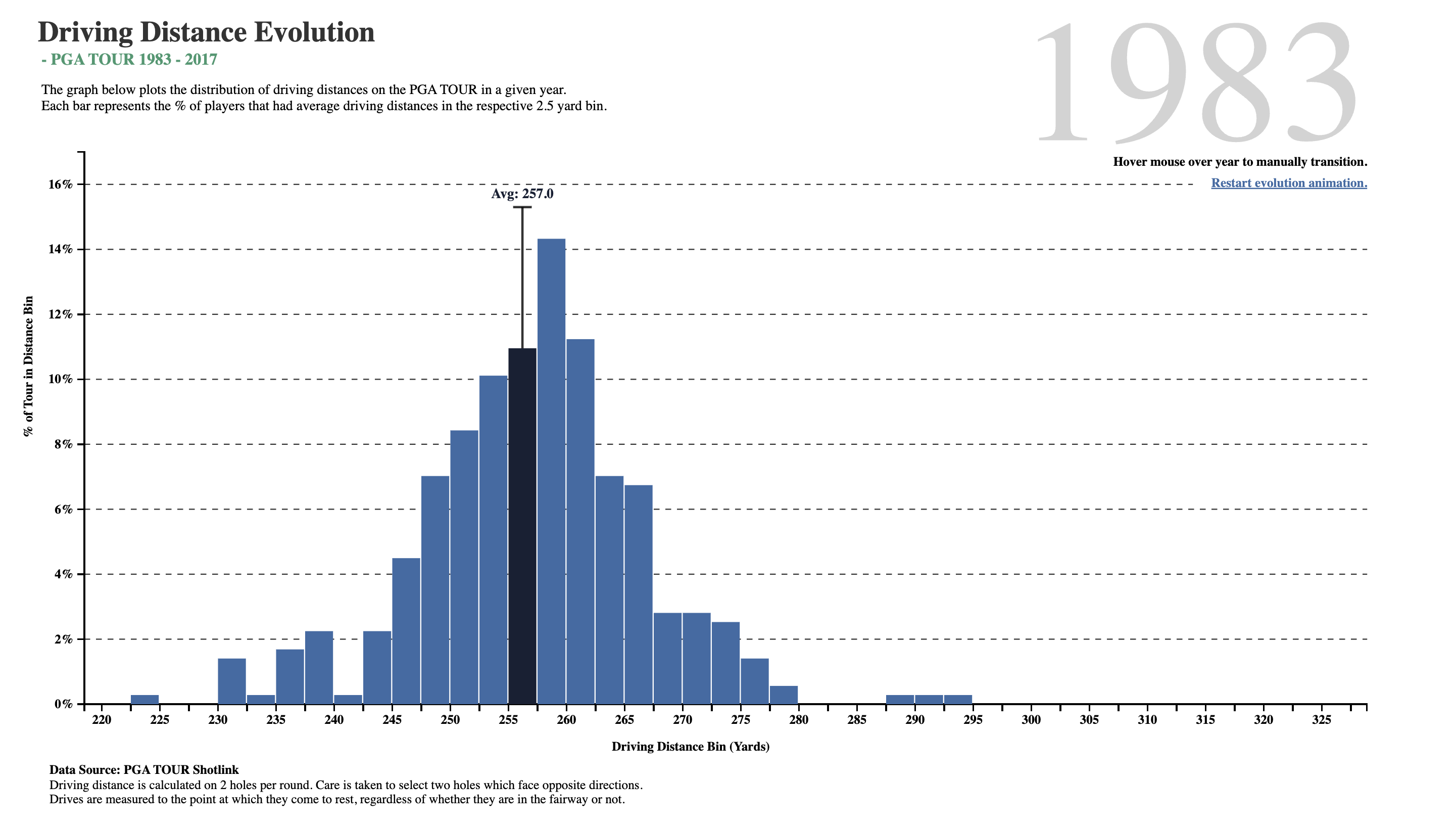
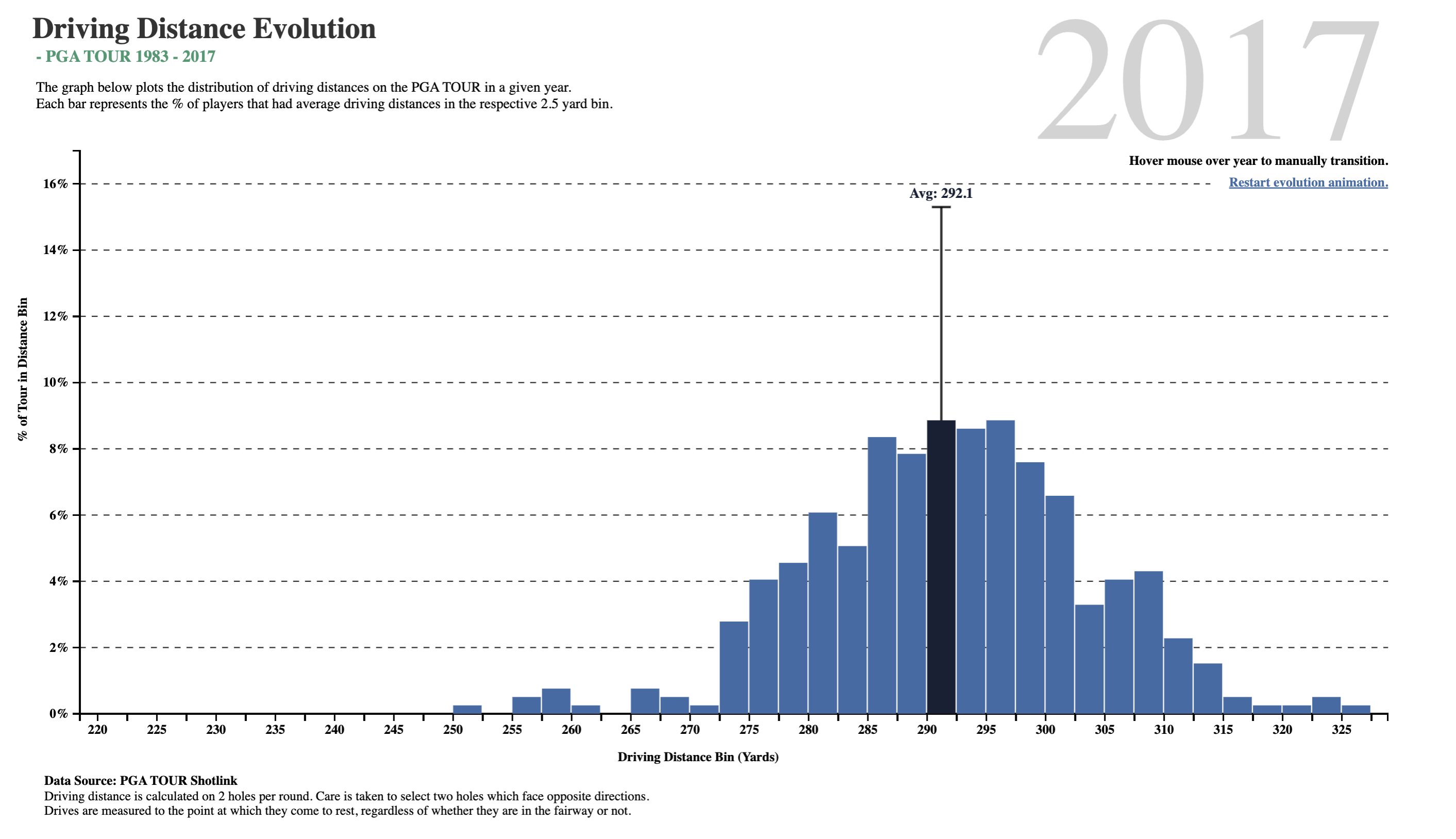
What do we see here? In about two-and-a-half decades, golf drive distances have increased, on the average, by 35 yards. The maximum distance has also gone up by 30 yards, and the minimum is now at 250 yards, which was close to average in 1983! What was a decent average in 1983 is just the bare minimum in 2017!!
Is it the dimples that the golf balls have? But these have been around a long time…or is it the clubs, and the swing technique invented by more recent players?
Hans Rosling’s famous Presentation
Now, let us listen to the late great Hans Rosling from the Gapminder Project, which aims at telling stories of the world with data, to remove systemic biases about poverty, income and gender related issues.
Histograms are best to show the distribution of raw Quantitative data, by displaying the number of values that fall within defined ranges, often called buckets or bins. We use a Quant variable on the x-axis and the histogram shows us how frequently different values occur for that variable by showing counts/frequencies on the y-axis. The x-axis is typically broken up into “buckets” or ranges for the x-variable. And usually you can adjust the bucket ranges to explore frequency patterns. For example, you can widen histogram buckets from 0-1, 1-2, 2-3, etc. to 0-2, 2-4, etc.
Although Bar Charts may look similar to Histograms, the two are different. Bar Charts show counts of observations with respect to a Qualitative variable. For instance, bar charts show categorical data with multiple levels, such as fruits, clothing, household products in an inventory. Each bar has a height proportional to the count per shirt-size, in this example.
Histograms do not usually show spaces between buckets because the buckets represent contiguous ranges, while bar charts show spaces to separate each (unconnected) category/level within a Qual variable.
diamonds dataset
We will first look at at a dataset that is directly available in R, the diamonds dataset. As always, we will use our munging process to clean up the data for analysis.
Rows: 53,940
Columns: 10
$ carat <dbl> 0.23, 0.21, 0.23, 0.29, 0.31, 0.24, 0.24, 0.26, 0.22, 0.23, 0.…
$ cut <ord> Ideal, Premium, Good, Premium, Good, Very Good, Very Good, Ver…
$ color <ord> E, E, E, I, J, J, I, H, E, H, J, J, F, J, E, E, I, J, J, J, I,…
$ clarity <ord> SI2, SI1, VS1, VS2, SI2, VVS2, VVS1, SI1, VS2, VS1, SI1, VS1, …
$ depth <dbl> 61.5, 59.8, 56.9, 62.4, 63.3, 62.8, 62.3, 61.9, 65.1, 59.4, 64…
$ table <dbl> 55, 61, 65, 58, 58, 57, 57, 55, 61, 61, 55, 56, 61, 54, 62, 58…
$ price <int> 326, 326, 327, 334, 335, 336, 336, 337, 337, 338, 339, 340, 34…
$ x <dbl> 3.95, 3.89, 4.05, 4.20, 4.34, 3.94, 3.95, 4.07, 3.87, 4.00, 4.…
$ y <dbl> 3.98, 3.84, 4.07, 4.23, 4.35, 3.96, 3.98, 4.11, 3.78, 4.05, 4.…
$ z <dbl> 2.43, 2.31, 2.31, 2.63, 2.75, 2.48, 2.47, 2.53, 2.49, 2.39, 2.…We have ~54000 observations, with 10 variables. There are no missing values in any variable. It is a nice mix of Quantitative and Qualitative variables.
Since the variables are nicely converted to factor where needed, and the names are already clean we will just use janitor to essentially rename our dataset.
Code
Rows: 53,940
Columns: 10
$ carat <dbl> 0.23, 0.21, 0.23, 0.29, 0.31, 0.24, 0.24, 0.26, 0.22, 0.23, 0.…
$ cut <ord> Ideal, Premium, Good, Premium, Good, Very Good, Very Good, Ver…
$ color <ord> E, E, E, I, J, J, I, H, E, H, J, J, F, J, E, E, I, J, J, J, I,…
$ clarity <ord> SI2, SI1, VS1, VS2, SI2, VVS2, VVS1, SI1, VS2, VS1, SI1, VS1, …
$ depth <dbl> 61.5, 59.8, 56.9, 62.4, 63.3, 62.8, 62.3, 61.9, 65.1, 59.4, 64…
$ table <dbl> 55, 61, 65, 58, 58, 57, 57, 55, 61, 61, 55, 56, 61, 54, 62, 58…
$ price <int> 326, 326, 327, 334, 335, 336, 336, 337, 337, 338, 339, 340, 34…
$ x <dbl> 3.95, 3.89, 4.05, 4.20, 4.34, 3.94, 3.95, 4.07, 3.87, 4.00, 4.…
$ y <dbl> 3.98, 3.84, 4.07, 4.23, 4.35, 3.96, 3.98, 4.11, 3.78, 4.05, 4.…
$ z <dbl> 2.43, 2.31, 2.31, 2.63, 2.75, 2.48, 2.47, 2.53, 2.49, 2.39, 2.…
As per our Workflow, we will look at the data using all the three methods we have seen.
Rows: 53,940
Columns: 10
$ carat <dbl> 0.23, 0.21, 0.23, 0.29, 0.31, 0.24, 0.24, 0.26, 0.22, 0.23, 0.…
$ cut <ord> Ideal, Premium, Good, Premium, Good, Very Good, Very Good, Ver…
$ color <ord> E, E, E, I, J, J, I, H, E, H, J, J, F, J, E, E, I, J, J, J, I,…
$ clarity <ord> SI2, SI1, VS1, VS2, SI2, VVS2, VVS1, SI1, VS2, VS1, SI1, VS1, …
$ depth <dbl> 61.5, 59.8, 56.9, 62.4, 63.3, 62.8, 62.3, 61.9, 65.1, 59.4, 64…
$ table <dbl> 55, 61, 65, 58, 58, 57, 57, 55, 61, 61, 55, 56, 61, 54, 62, 58…
$ price <int> 326, 326, 327, 334, 335, 336, 336, 337, 337, 338, 339, 340, 34…
$ x <dbl> 3.95, 3.89, 4.05, 4.20, 4.34, 3.94, 3.95, 4.07, 3.87, 4.00, 4.…
$ y <dbl> 3.98, 3.84, 4.07, 4.23, 4.35, 3.96, 3.98, 4.11, 3.78, 4.05, 4.…
$ z <dbl> 2.43, 2.31, 2.31, 2.63, 2.75, 2.48, 2.47, 2.53, 2.49, 2.39, 2.…| Name | diamonds_modified |
| Number of rows | 53940 |
| Number of columns | 10 |
| _______________________ | |
| Column type frequency: | |
| factor | 3 |
| numeric | 7 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| cut | 0 | 1 | TRUE | 5 | Ide: 21551, Pre: 13791, Ver: 12082, Goo: 4906 |
| color | 0 | 1 | TRUE | 7 | G: 11292, E: 9797, F: 9542, H: 8304 |
| clarity | 0 | 1 | TRUE | 8 | SI1: 13065, VS2: 12258, SI2: 9194, VS1: 8171 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| carat | 0 | 1 | 0.80 | 0.47 | 0.2 | 0.40 | 0.70 | 1.04 | 5.01 | ▇▂▁▁▁ |
| depth | 0 | 1 | 61.75 | 1.43 | 43.0 | 61.00 | 61.80 | 62.50 | 79.00 | ▁▁▇▁▁ |
| table | 0 | 1 | 57.46 | 2.23 | 43.0 | 56.00 | 57.00 | 59.00 | 95.00 | ▁▇▁▁▁ |
| price | 0 | 1 | 3932.80 | 3989.44 | 326.0 | 950.00 | 2401.00 | 5324.25 | 18823.00 | ▇▂▁▁▁ |
| x | 0 | 1 | 5.73 | 1.12 | 0.0 | 4.71 | 5.70 | 6.54 | 10.74 | ▁▁▇▃▁ |
| y | 0 | 1 | 5.73 | 1.14 | 0.0 | 4.72 | 5.71 | 6.54 | 58.90 | ▇▁▁▁▁ |
| z | 0 | 1 | 3.54 | 0.71 | 0.0 | 2.91 | 3.53 | 4.04 | 31.80 | ▇▁▁▁▁ |
categorical variables:
name class levels n missing
1 cut ordered 5 53940 0
2 color ordered 7 53940 0
3 clarity ordered 8 53940 0
distribution
1 Ideal (40%), Premium (25.6%) ...
2 G (20.9%), E (18.2%), F (17.7%) ...
3 SI1 (24.2%), VS2 (22.7%), SI2 (17%) ...
quantitative variables:
name class min Q1 median Q3 max mean sd
1 carat numeric 0.2 0.40 0.70 1.04 5.01 0.7979397 0.4740112
2 depth numeric 43.0 61.00 61.80 62.50 79.00 61.7494049 1.4326213
3 table numeric 43.0 56.00 57.00 59.00 95.00 57.4571839 2.2344906
4 price integer 326.0 950.00 2401.00 5324.25 18823.00 3932.7997219 3989.4397381
5 x numeric 0.0 4.71 5.70 6.54 10.74 5.7311572 1.1217607
6 y numeric 0.0 4.72 5.71 6.54 58.90 5.7345260 1.1421347
7 z numeric 0.0 2.91 3.53 4.04 31.80 3.5387338 0.7056988
n missing
1 53940 0
2 53940 0
3 53940 0
4 53940 0
5 53940 0
6 53940 0
7 53940 0
Quantitative Data
carat(dbl): weight of the diamond 0.2-5.01depth(dbl): depth total depth percentage 43-79table(dbl): width of top of diamond relative to widest point 43-95price(dbl): price in US dollars $326-$18,823x(dbl): length in mm 0-10.74y(dbl): width in mm 0-58.9z(dbl): depth in mm 0-31.8
Qualitative Data
cut: diamond cut Fair, Good, Very Good, Premium, Ideal color: diamond color J (worst) to D (best). (7 levels) clarity. measurement of how clear the diamond is I1 (worst), SI2, SI1, VS2, VS1, VVS2, VVS1, IF (best).
These have 5, 7, and 8 levels respectively. The fact that the class for these is ordered suggests that these are factors and that the levels have a sequence/order.
Business Insights on Examining the diamonds dataset
- This is a large dataset (54K rows).
- There are several Qualitative variables:
carat,price,x,y,z,depthandtableare Quantitative variables.- There are no missing values for any variable, all are complete with 54K entries.
Let us formulate a few Questions about this dataset. At some point, we might develop a hunch or two, and these would become our hypotheses to investigate. This is an iterative process!
Hypothesis and Research Questions
- The
target variablefor an experiment that resulted in this data might be thepricevariable. Which is a numerical Quant variable.
- There are also
predictor variablessuch ascarat(Quant),color(Qual),cut(Qual), andclarity(Qual).
- Other
predictor variablesmight bex, y, depth, table(all Quant)
- Research Questions:
- What is the distribution of the target variable
price? - What is the distribution of the predictor variable
carat? - Does a
pricedistribution vary based upon type ofcut,clarity, andcolor?
- What is the distribution of the target variable
These should do for now. Try and think of more Questions!
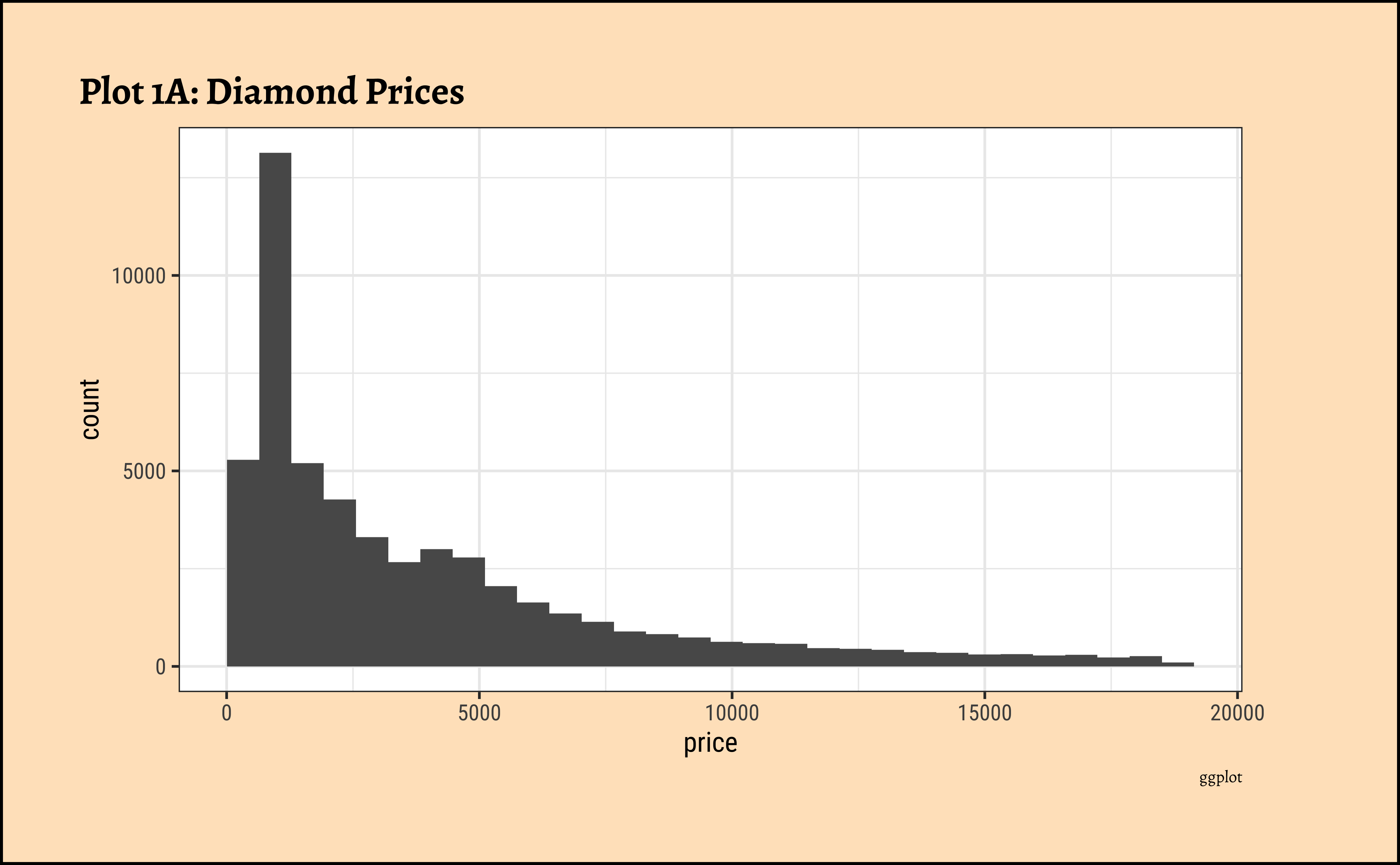
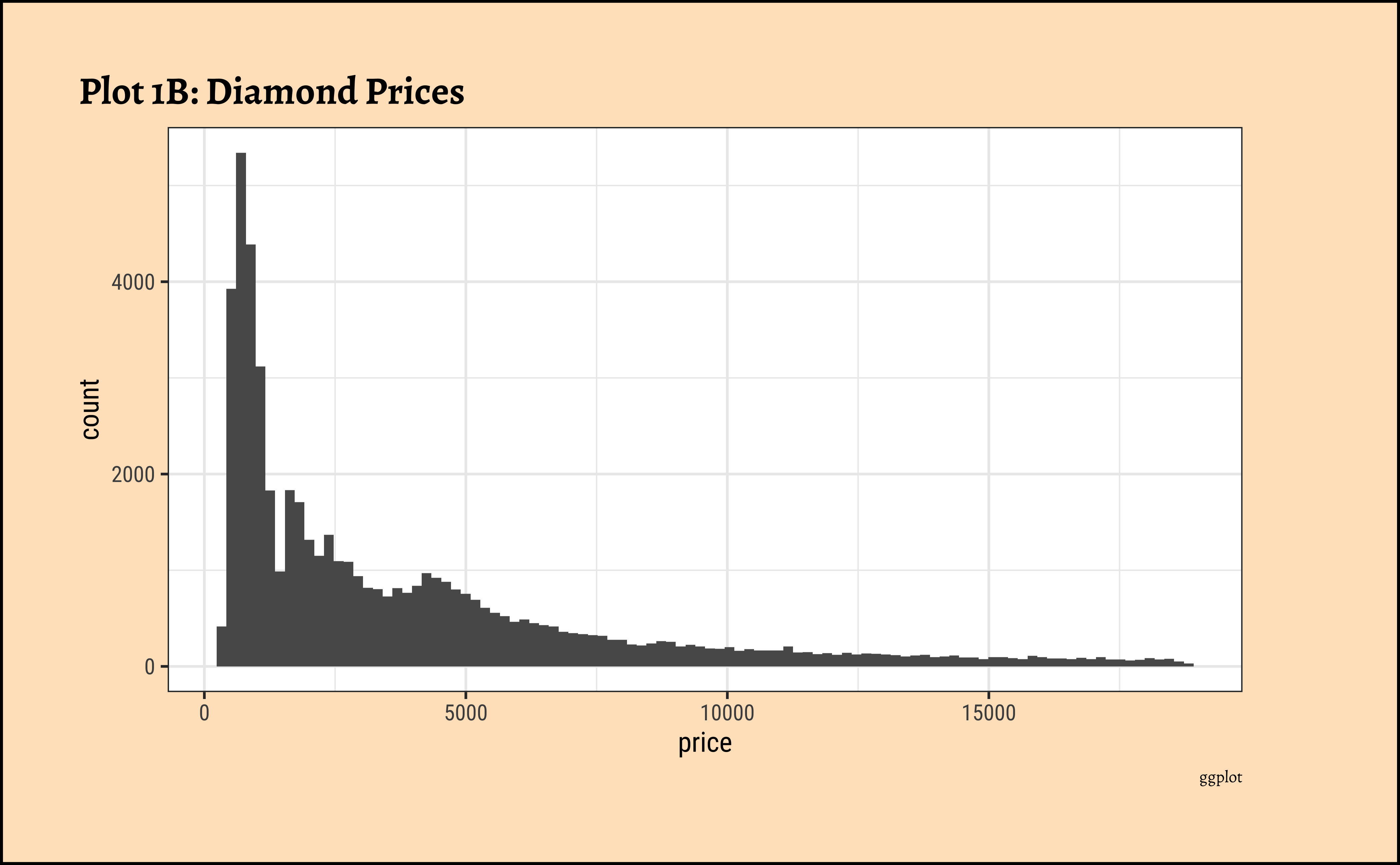
Let’s plot some histograms to answer each of the Hypothesis questions above.
price?
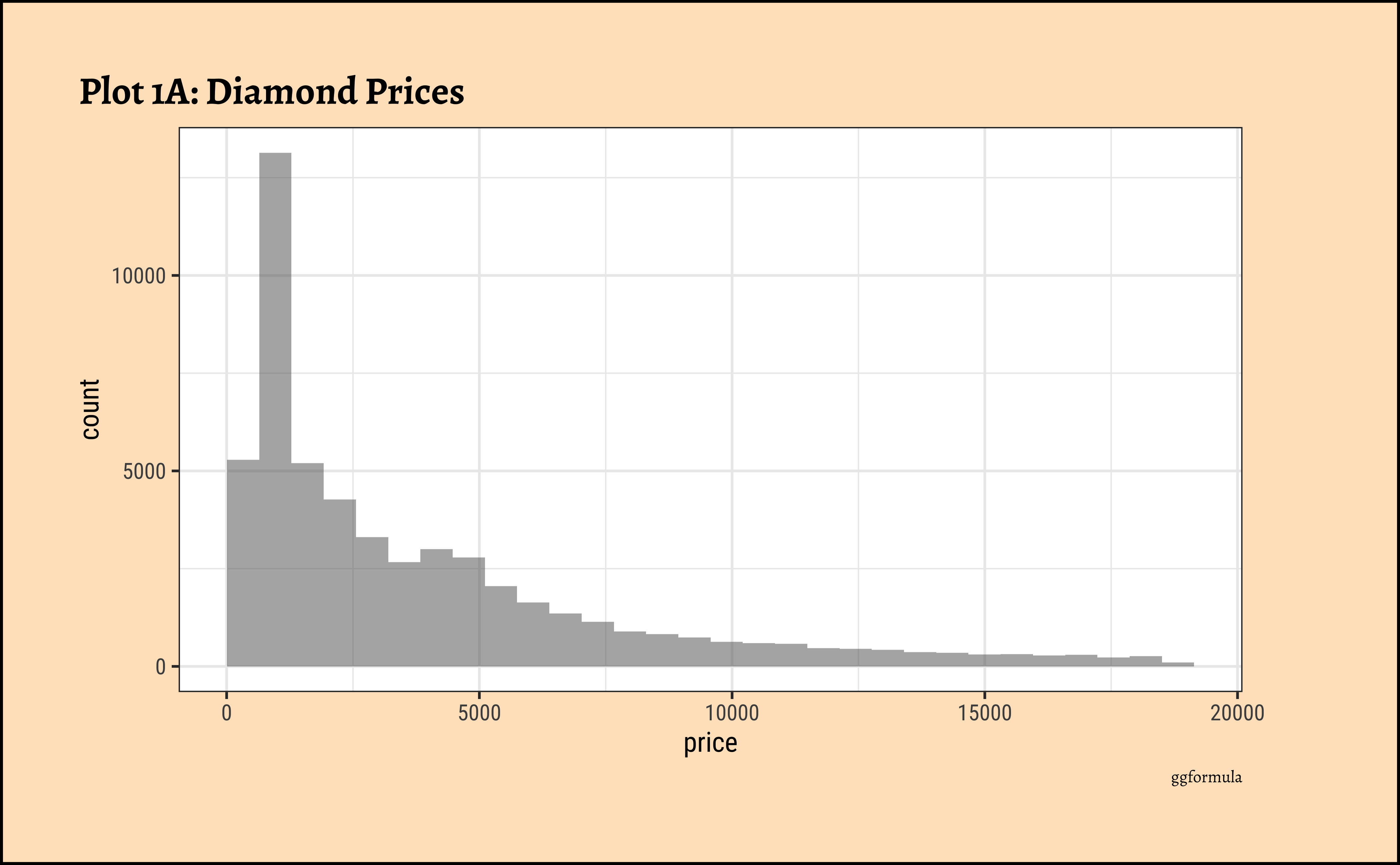
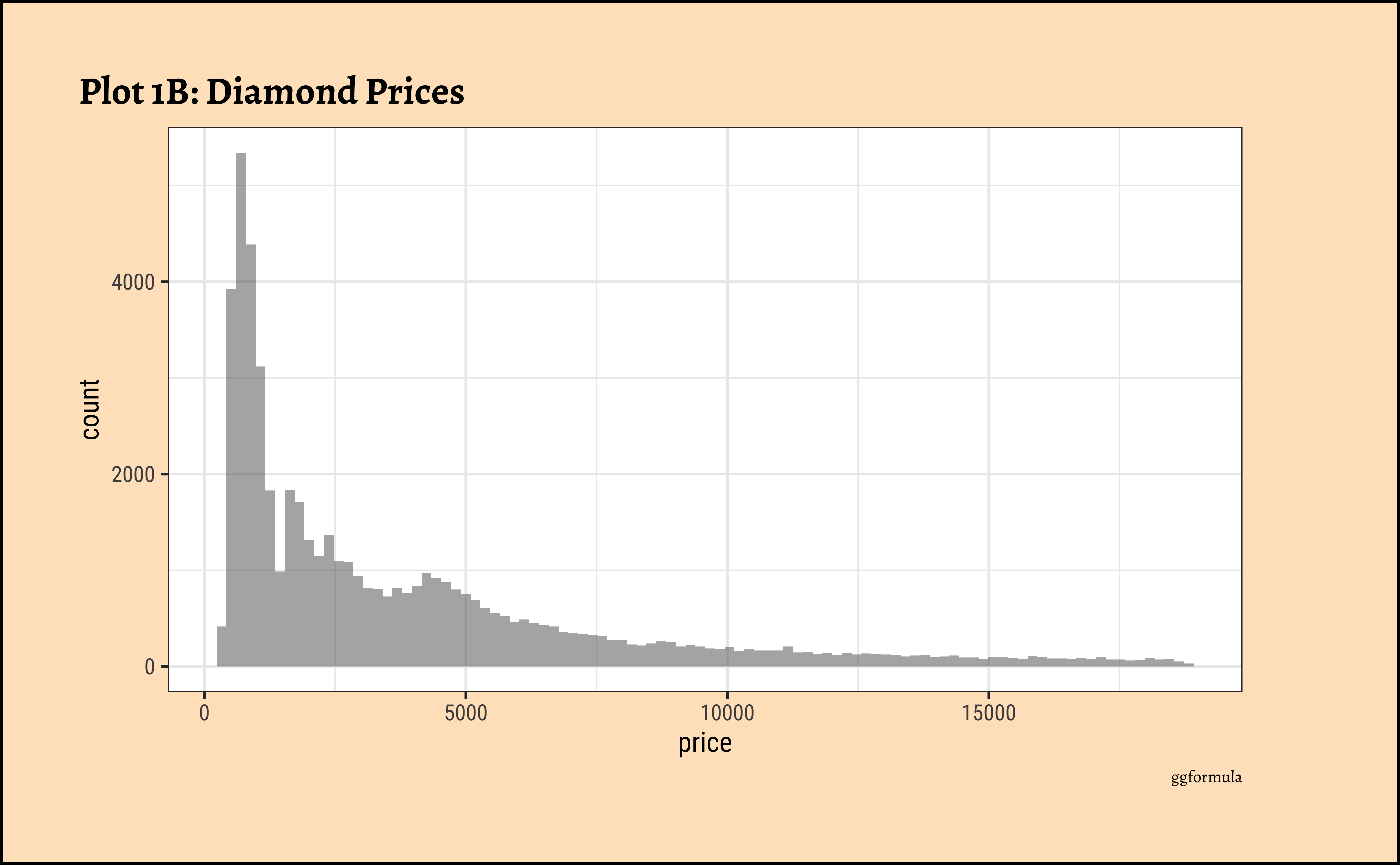
- The
pricedistribution is heavily skewed to the right.
- There are a great many diamonds at relatively low prices, but there are a good few diamonds at very high prices too.
- Using a high number of bins does not materially change the view of the histogram.
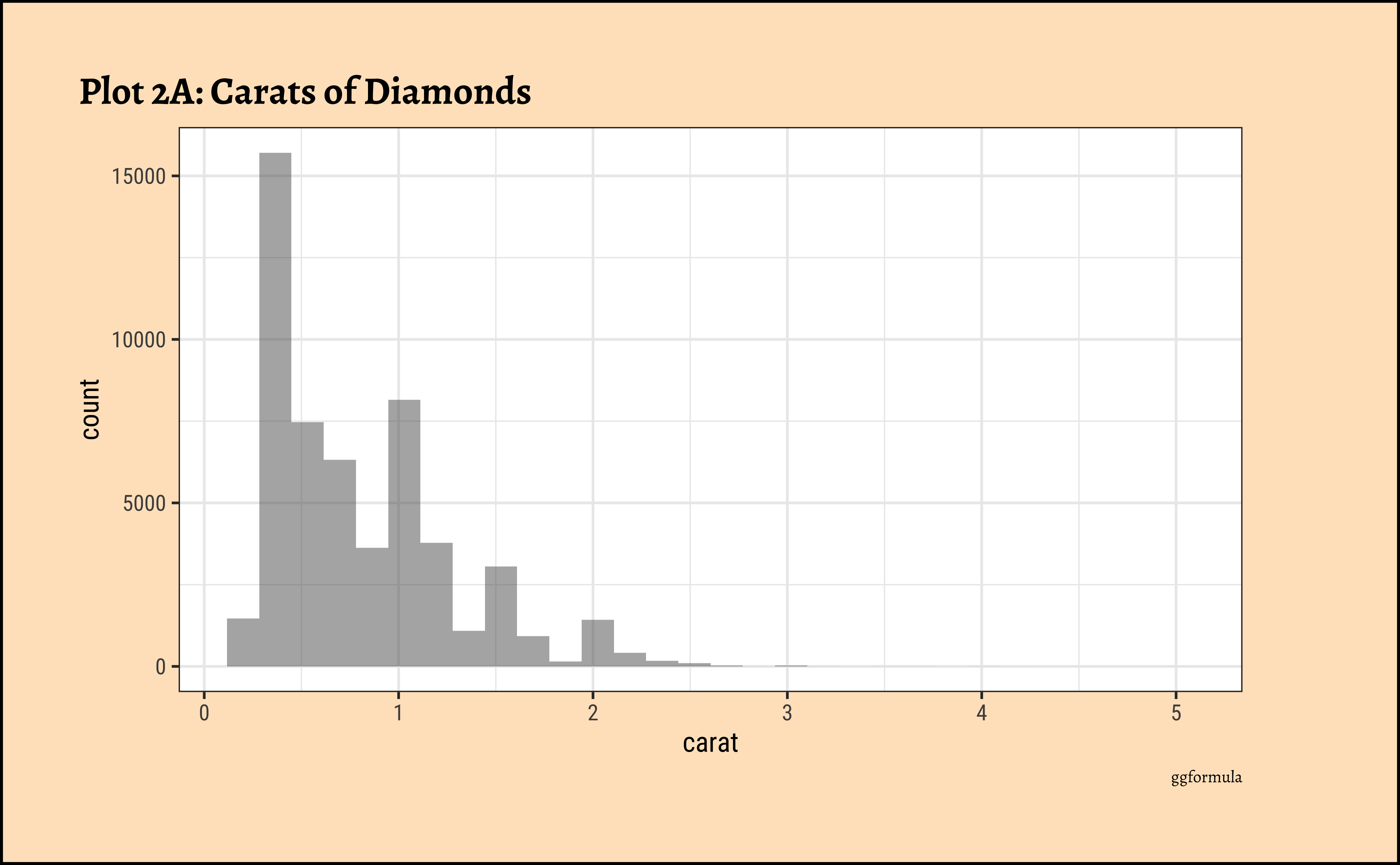
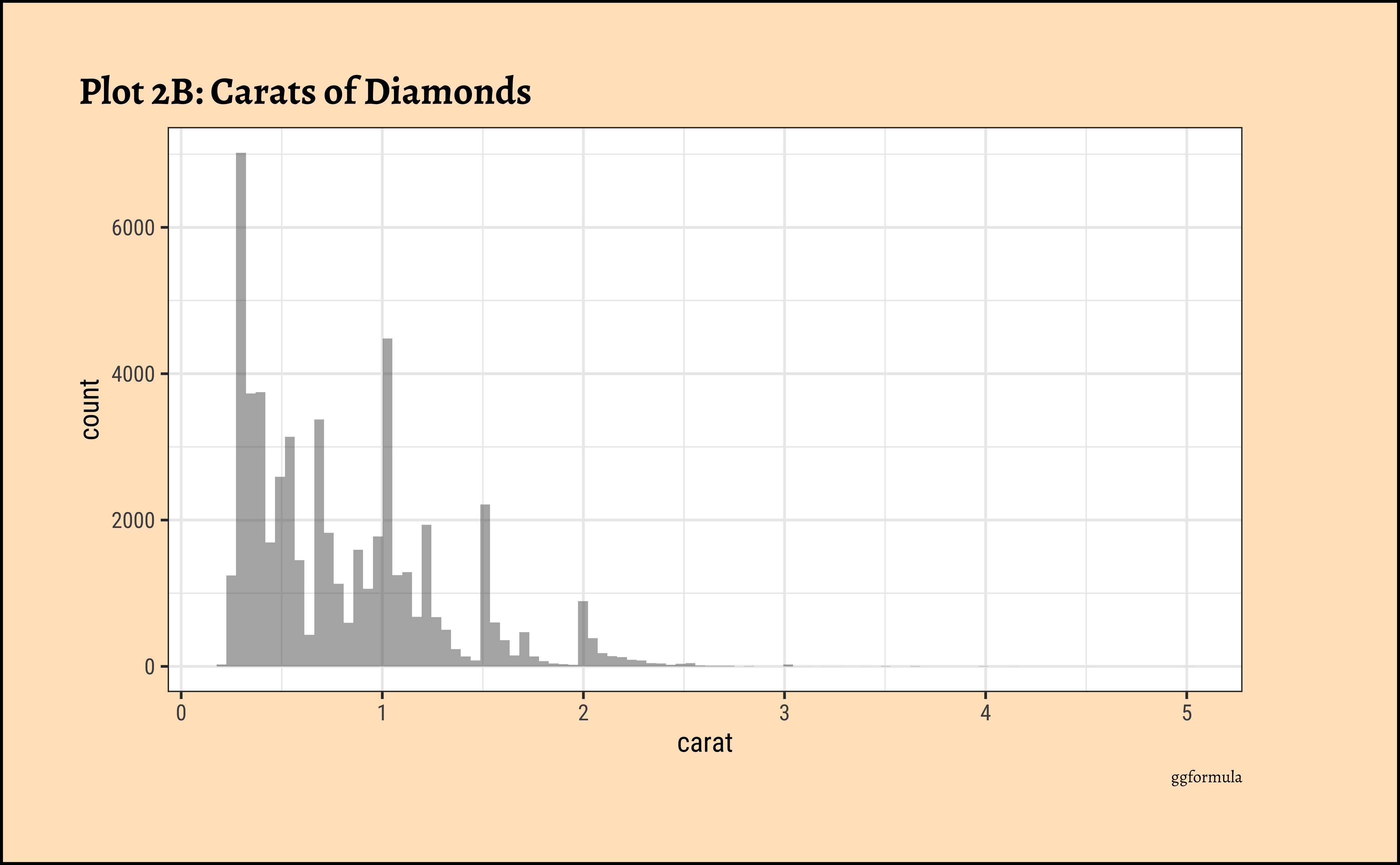
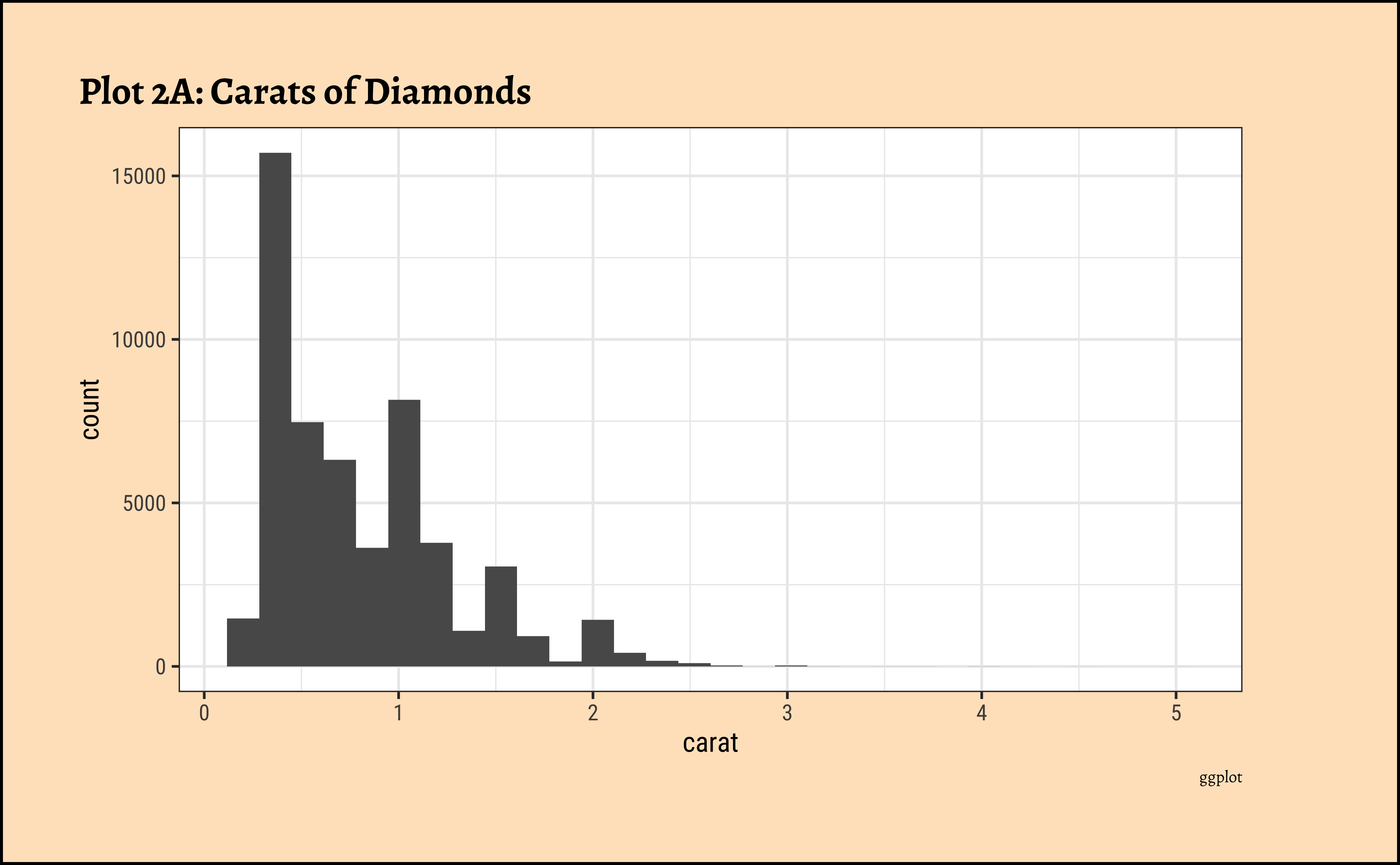
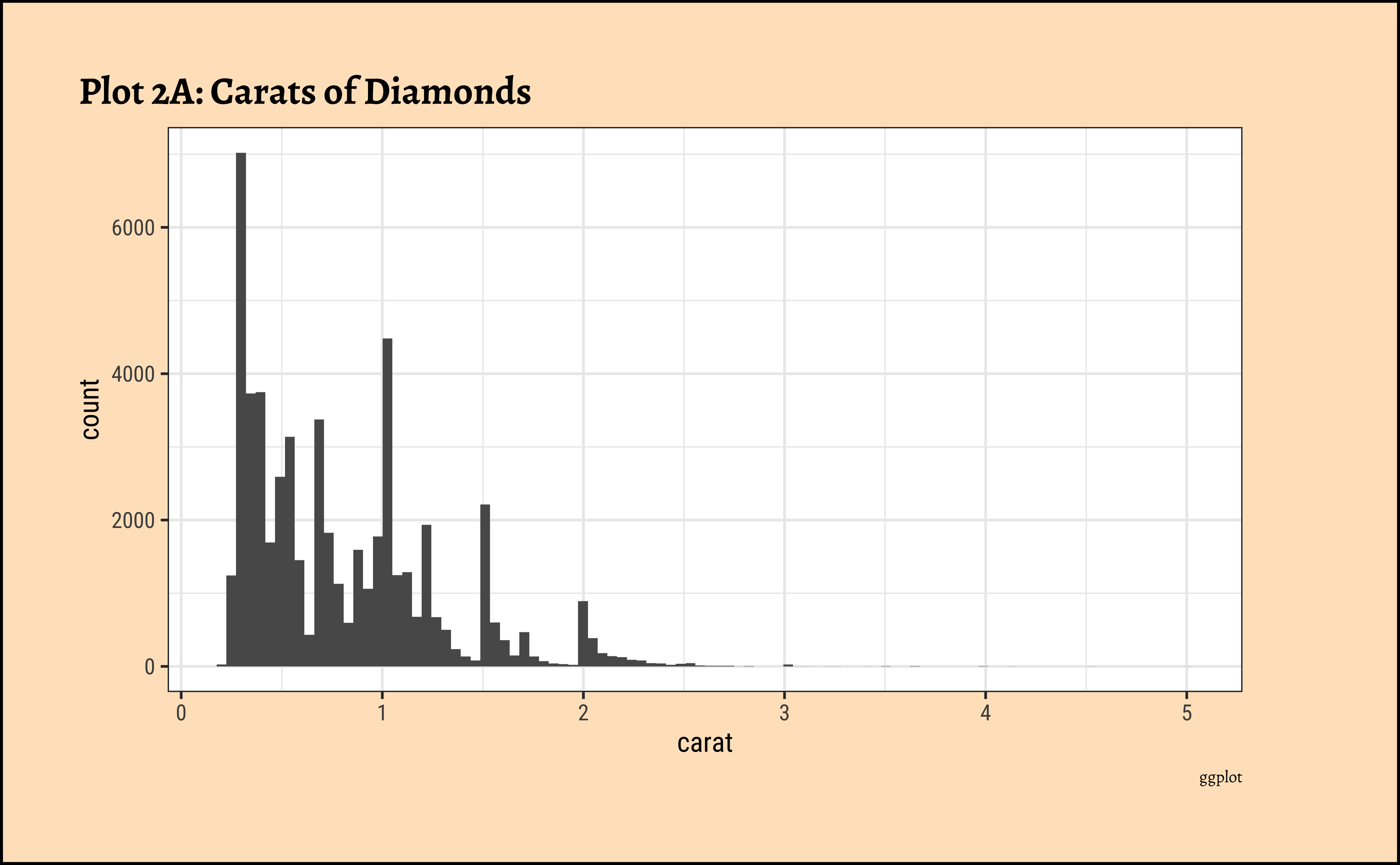
carat?
ggplot2::theme_set(new = theme_custom())
diamonds_modified %>%
ggplot() +
geom_histogram(aes(x = carat)) +
labs(
title = "Plot 2A: Carats of Diamonds",
caption = "ggplot"
)
## More bins
diamonds_modified %>%
ggplot() +
geom_histogram(aes(x = carat), bins = 100) +
labs(
title = "Plot 2A: Carats of Diamonds",
caption = "ggplot"
)caratalso has a heavily right-skewed distribution.
- However, there is a marked “discreteness” to the distribution. Some values of carat are far more common than others. For example, 1, 1.5, and 2 carat diamonds are large in number.
- Why does the X-axis extend up to 5 carats? There must be some, very few, diamonds of very high carat value!
price distribution vary based upon type of cut, clarity, and color?
ggplot2::theme_set(new = theme_custom())
diamonds_modified %>%
gf_histogram(~price, fill = ~cut, color = "black", alpha = 0.3) %>%
gf_facet_wrap(~cut) %>%
gf_labs(
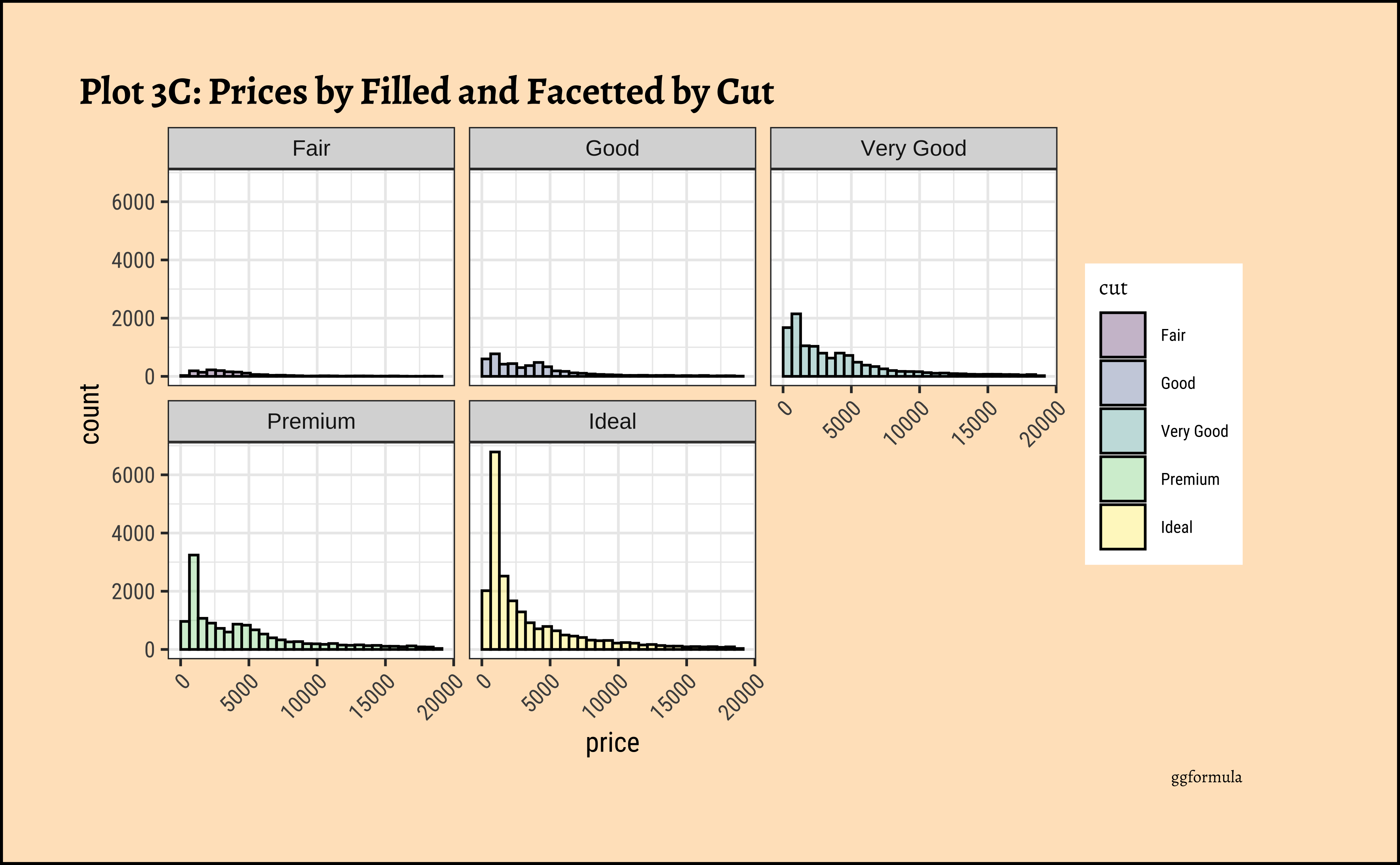
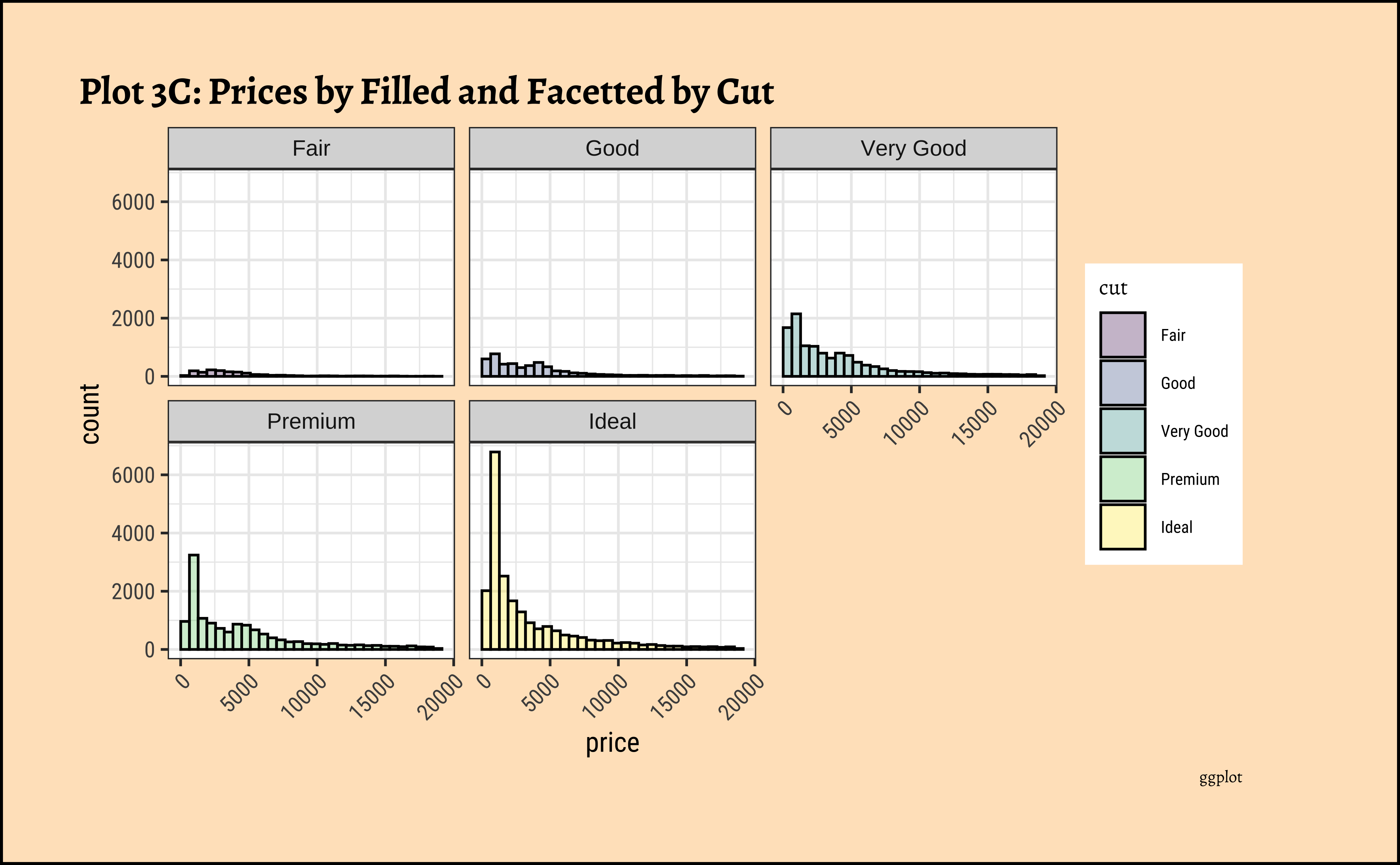
title = "Plot 3C: Prices by Filled and Facetted by Cut",
caption = "ggformula"
) %>%
gf_theme(theme(
axis.text.x = element_text(
angle = 45,
hjust = 1
)
))ggplot2::theme_set(new = theme_custom())
diamonds_modified %>%
gf_histogram(~price, fill = ~cut, color = "black", alpha = 0.3) %>%
gf_facet_wrap(~cut, scales = "free_y", nrow = 2) %>%
gf_labs(
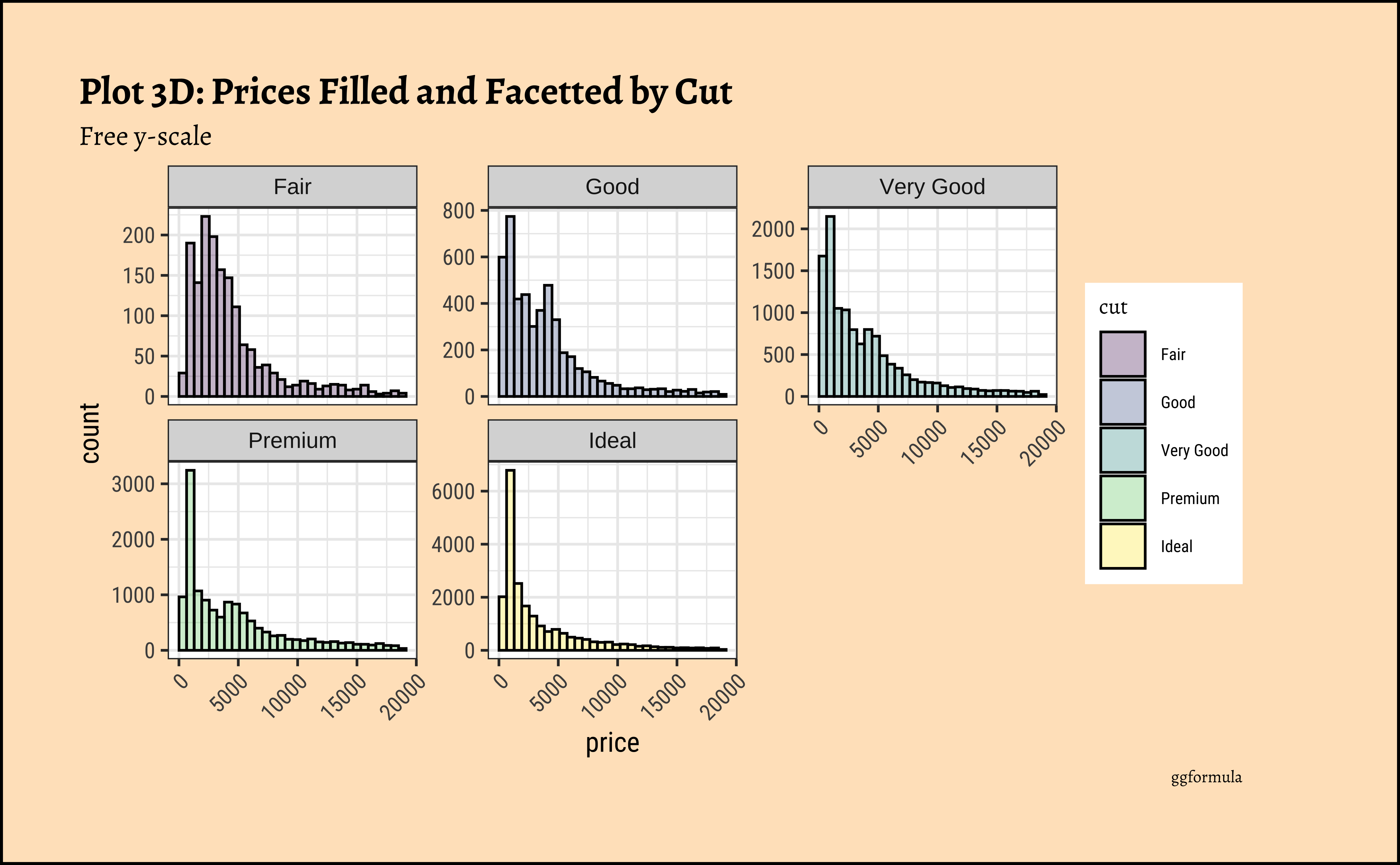
title = "Plot 3D: Prices Filled and Facetted by Cut",
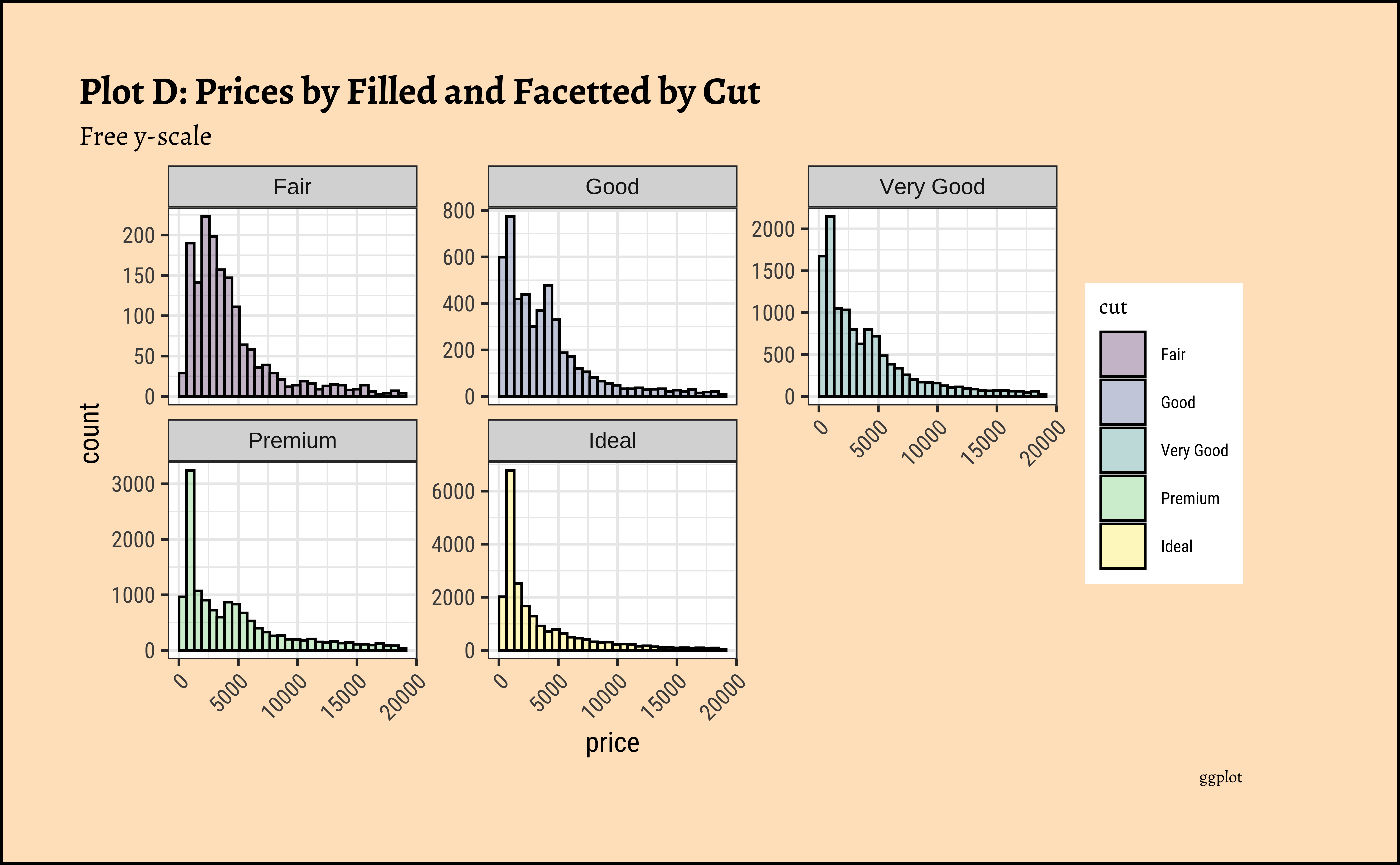
subtitle = "Free y-scale",
caption = "ggformula"
) %>%
gf_theme(theme(
axis.text.x =
element_text(
angle = 45,
hjust = 1
)
))ggplot2::theme_set(new = theme_custom())
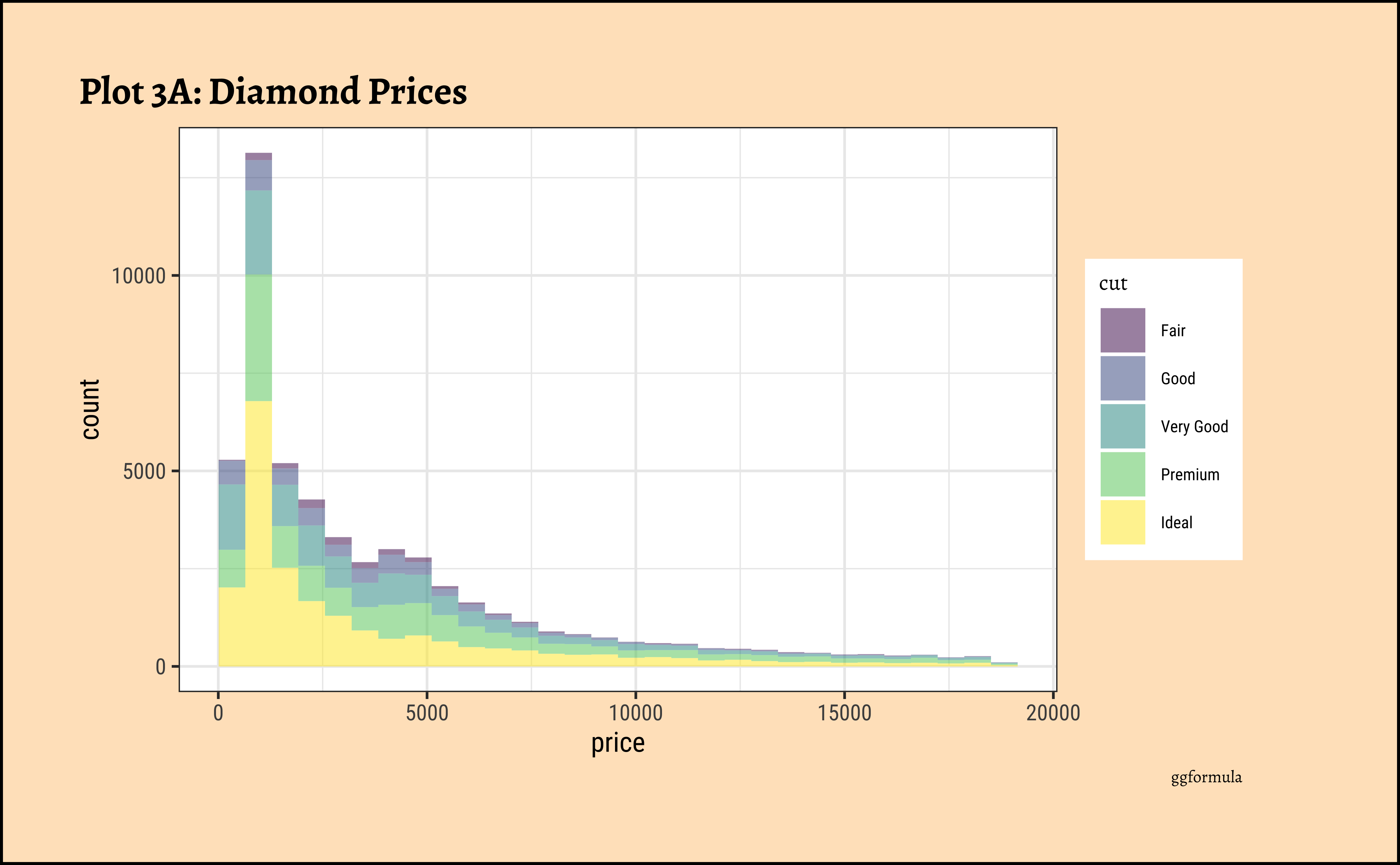
diamonds_modified %>% ggplot() +
geom_histogram(aes(x = price, fill = cut), alpha = 0.3) +
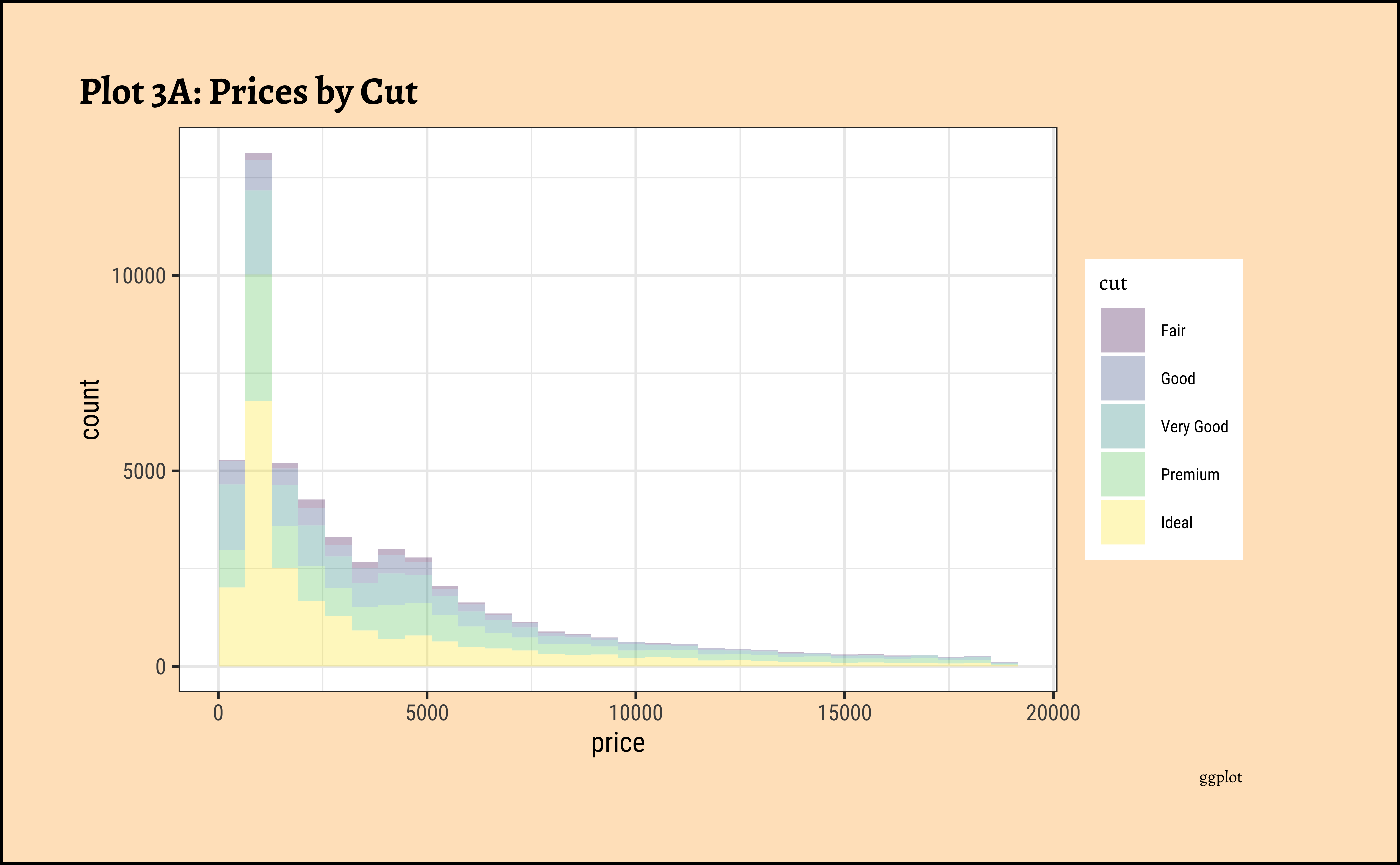
labs(title = "Plot 3A: Prices by Cut", caption = "ggplot")
##
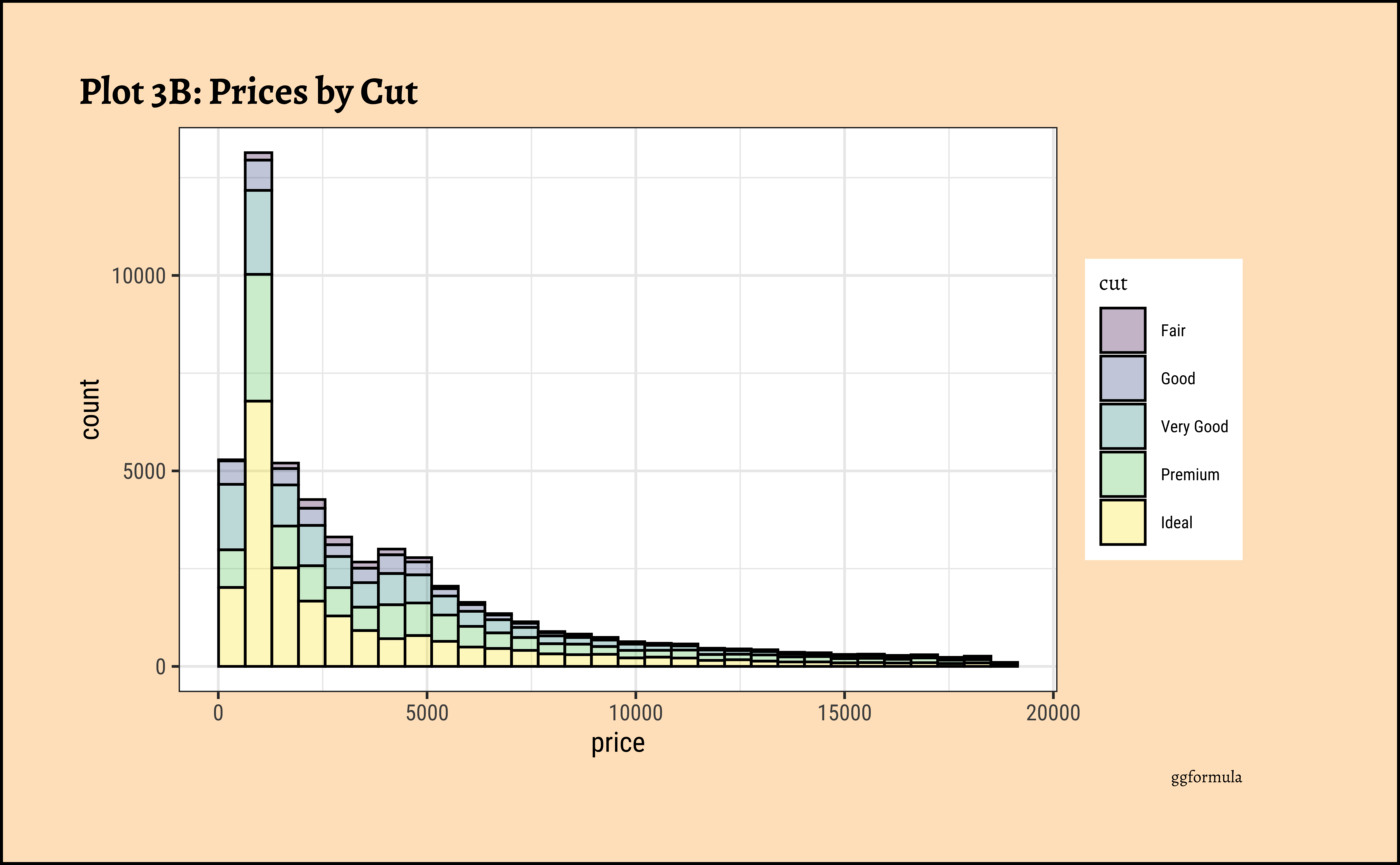
diamonds_modified %>%
ggplot() +
geom_histogram(aes(x = price, fill = cut),
colour = "black", alpha = 0.3
) +
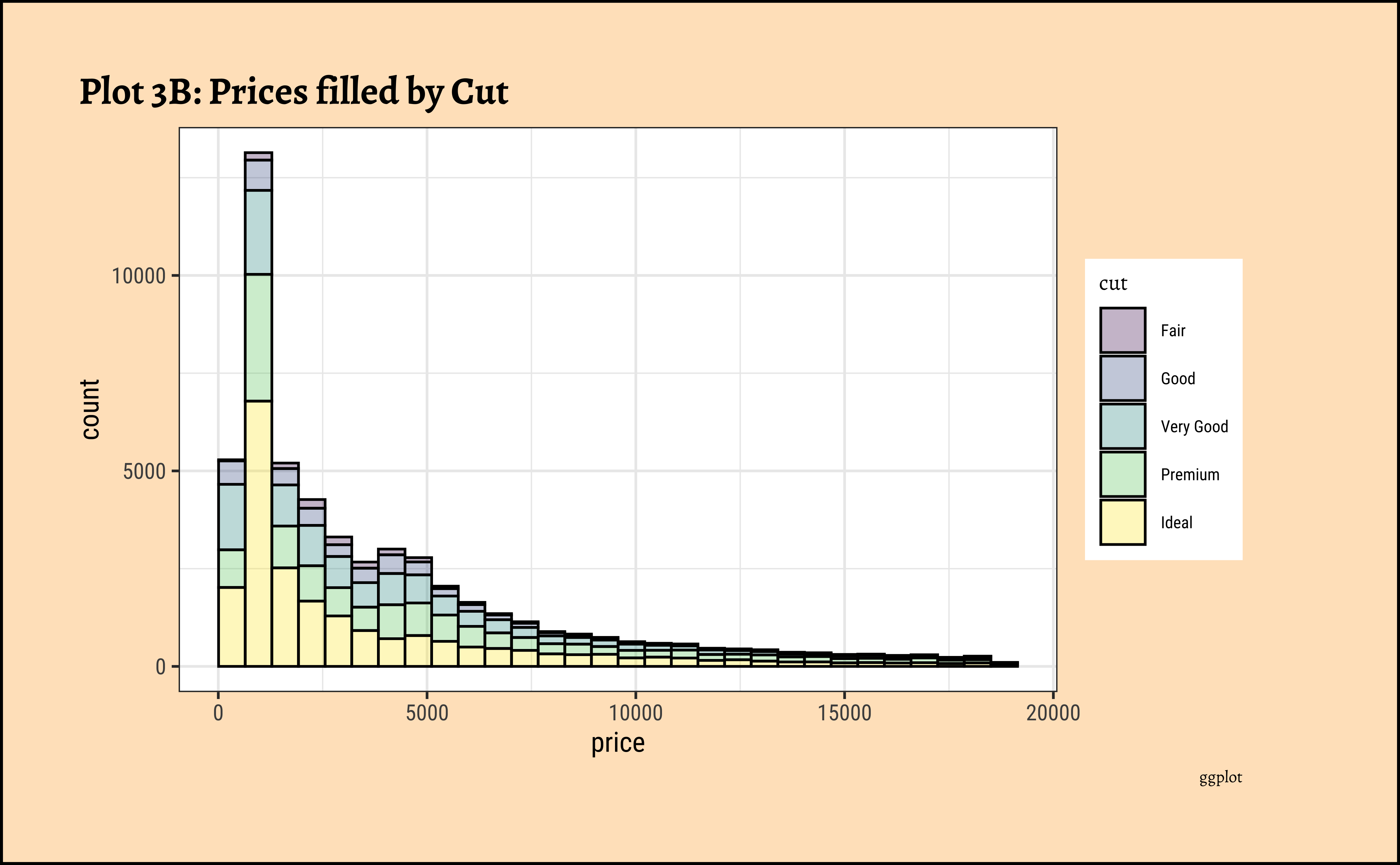
labs(title = "Plot 3B: Prices filled by Cut", caption = "ggplot")
##
diamonds_modified %>% ggplot() +
geom_histogram(aes(price, fill = cut),
colour = "black", alpha = 0.3
) +
facet_wrap(facets = vars(cut)) +
labs(
title = "Plot 3C: Prices by Filled and Facetted by Cut",
caption = "ggplot"
) +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
##
diamonds_modified %>% ggplot() +
geom_histogram(aes(price, fill = cut),
colour = "black", alpha = 0.3
) +
facet_wrap(facets = vars(cut), scales = "free_y") +
labs(
title = "Plot D: Prices by Filled and Facetted by Cut",
subtitle = "Free y-scale",
caption = "ggplot"
) +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
gf_histogram(~ price, fill = ~ cut, data = diamonds_modified) %>%
gf_labs(title = "Plot 3A: Diamond Prices",caption = "ggformula")
###
diamonds_modified %>%
gf_histogram(~ price, fill = ~ cut, color = "black", alpha = 0.3) %>%
gf_labs(title = "Plot 3B: Prices by Cut",
caption = "ggformula")
###
diamonds_modified %>%
gf_histogram(~ price, fill = ~ cut, color = "black", alpha = 0.3) %>%
gf_facet_wrap(~ cut) %>%
gf_labs(title = "Plot 3C: Prices by Filled and Facetted by Cut",
caption = "ggformula") %>%
gf_theme(theme(axis.text.x = element_text(angle = 45, hjust = 1)))
###
diamonds_modified %>%
gf_histogram(~ price, fill = ~ cut, color = "black", alpha = 0.3) %>%
gf_facet_wrap(~ cut, scales = "free_y", nrow = 2) %>%
gf_labs(title = "Plot 3D: Prices Filled and Facetted by Cut",
subtitle = "Free y-scale",
caption = "ggformula") %>%
gf_theme(theme(axis.text.x = element_text(angle = 45, hjust = 1)))- The price distribution is heavily skewed to the right AND This
long-tailednature of the histogram holds true regardless of thecutof the diamond. - See the x-axis range for each plot in Plot D! Price ranges are the same regardless of cut !! Very surprising! So
cutis perhaps not the only thing that determines price… - Facetting the plot into small multiples helps look at patterns better: overlapping histograms are hard to decipher. Adding
colordefines the bars in the histogram very well.
A Hypothesis
- The surprise insight above should lead you to make a Hypothesis!
- You should decide whether you want to investigate this question further, making more graphs, as we will see. Here, we are making a Hypothesis that more than just
cutdetermines thepriceof a diamond.
An Interactive App for Histograms
Type in your Console:
Before we conclude, let us look at a real world dataset: populations of countries. This dataset was taken from Kaggle https://www.kaggle.com/datasets/ulrikthygepedersen/populations. Click on the icon below to save the file into a subfolder called data in your project folder.
Rows: 16,400
Columns: 4
$ country_code <chr> "ABW", "ABW", "ABW", "ABW", "ABW", "ABW", "ABW", "ABW", "…
$ country_name <chr> "Aruba", "Aruba", "Aruba", "Aruba", "Aruba", "Aruba", "Ar…
$ year <dbl> 1960, 1961, 1962, 1963, 1964, 1965, 1966, 1967, 1968, 196…
$ value <dbl> 54608, 55811, 56682, 57475, 58178, 58782, 59291, 59522, 5…Real World Histograms
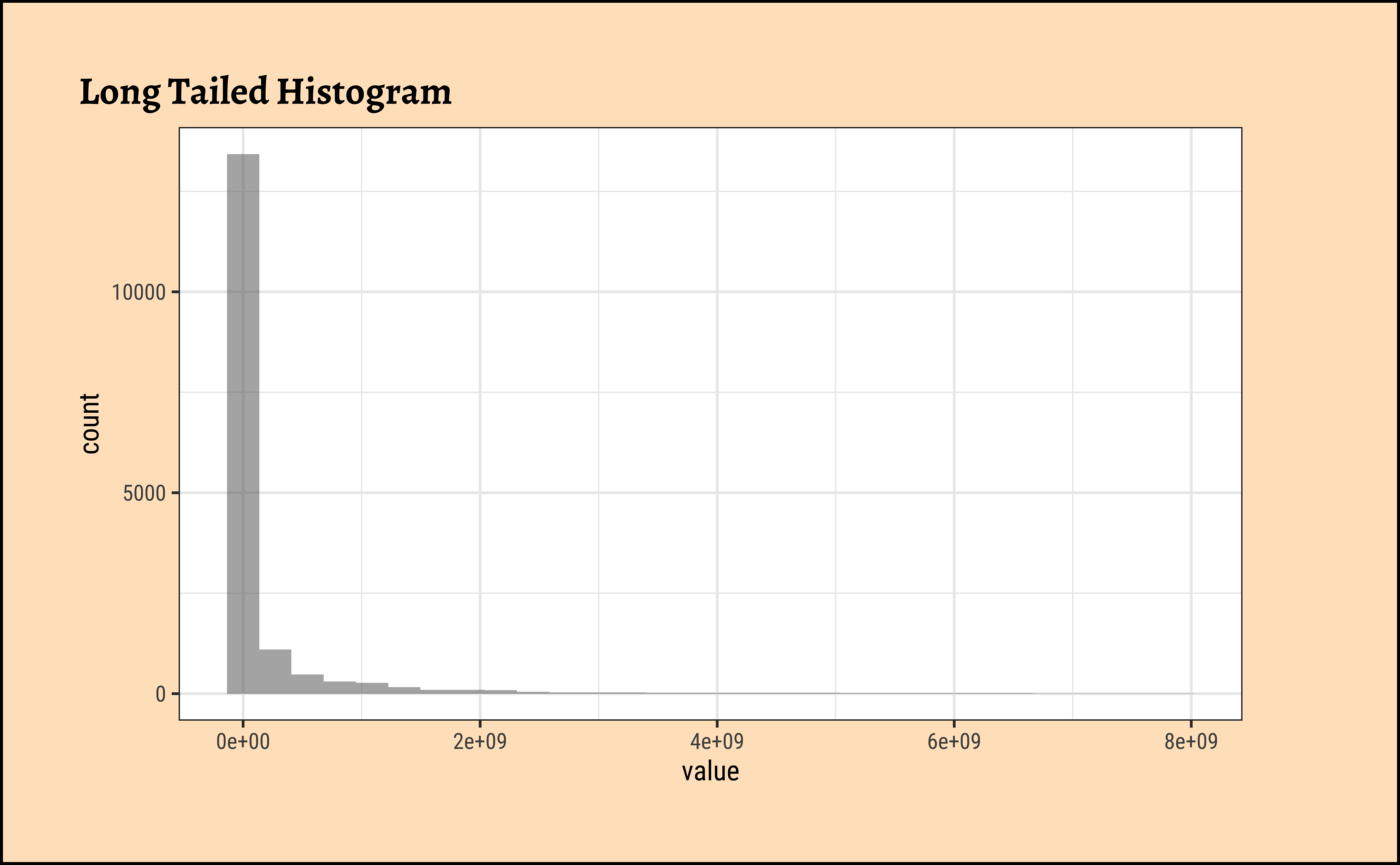
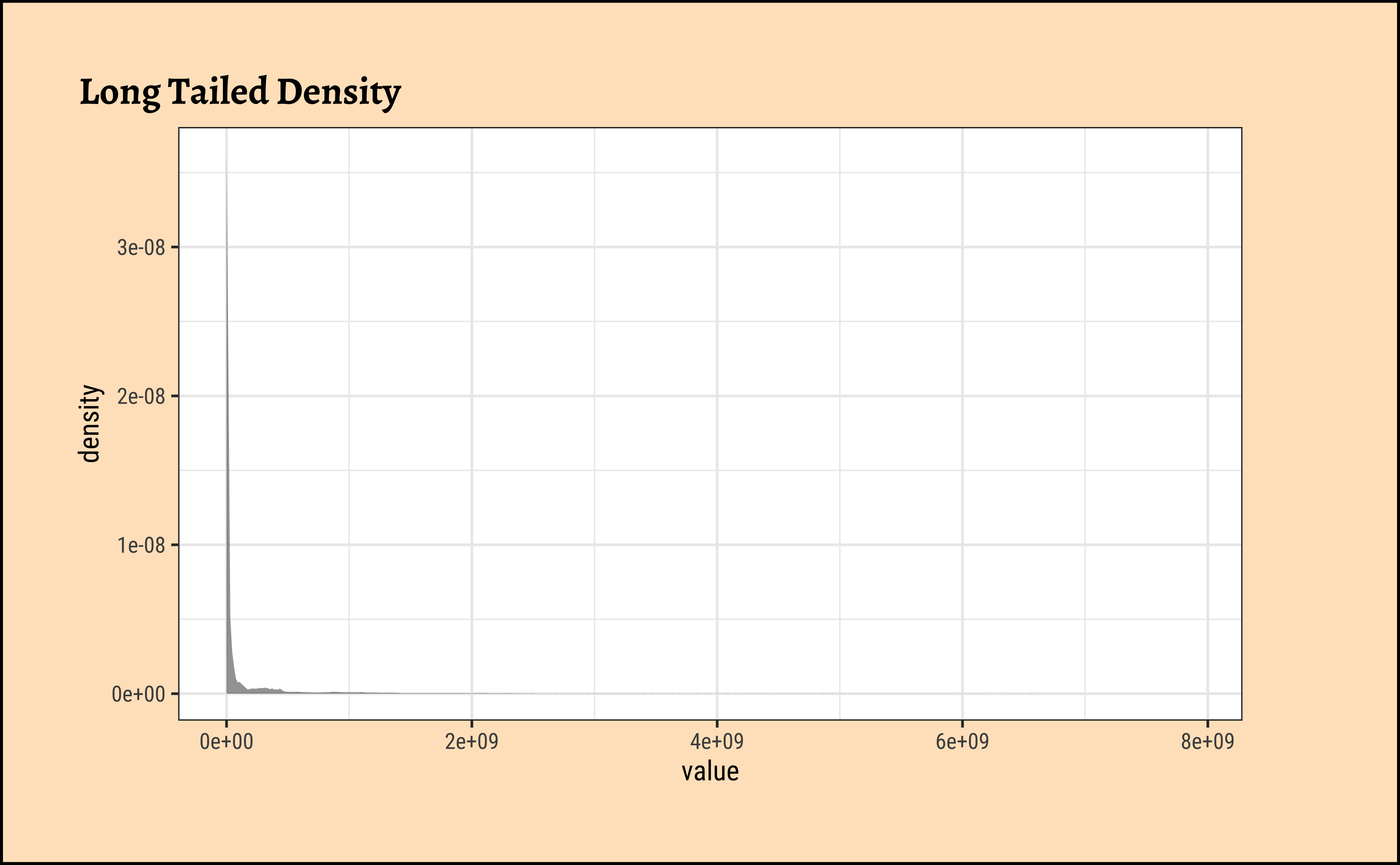
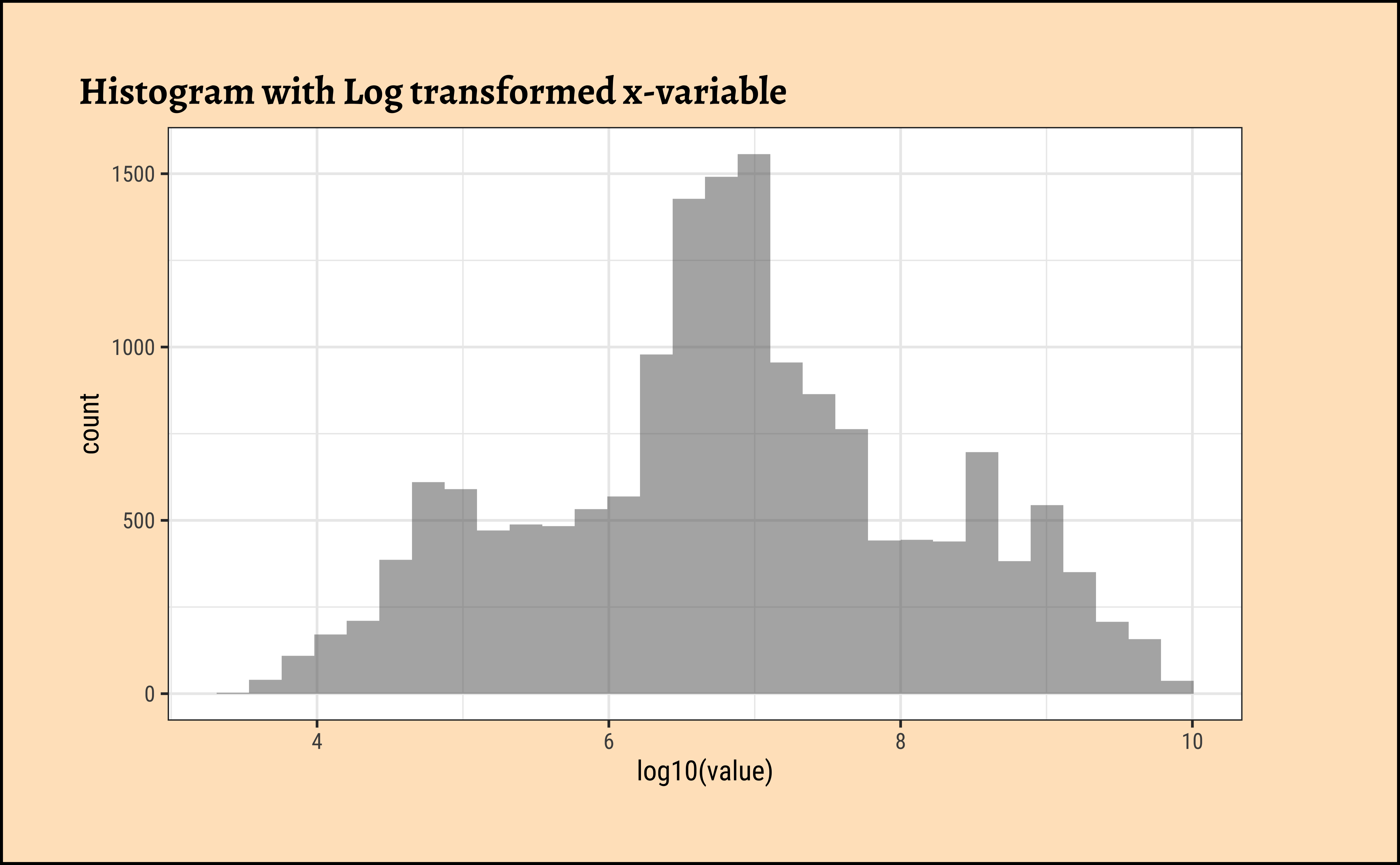
The value variable in this dataset is the population of a country. Let us plot densities/histograms for value:
Code
These graphs convey very little to us: the data is very heavily skewed to the right and much of the chart is empty. There are many countries with small populations and a few countries with very large populations. Such distributions are also called “long tailed” distributions.
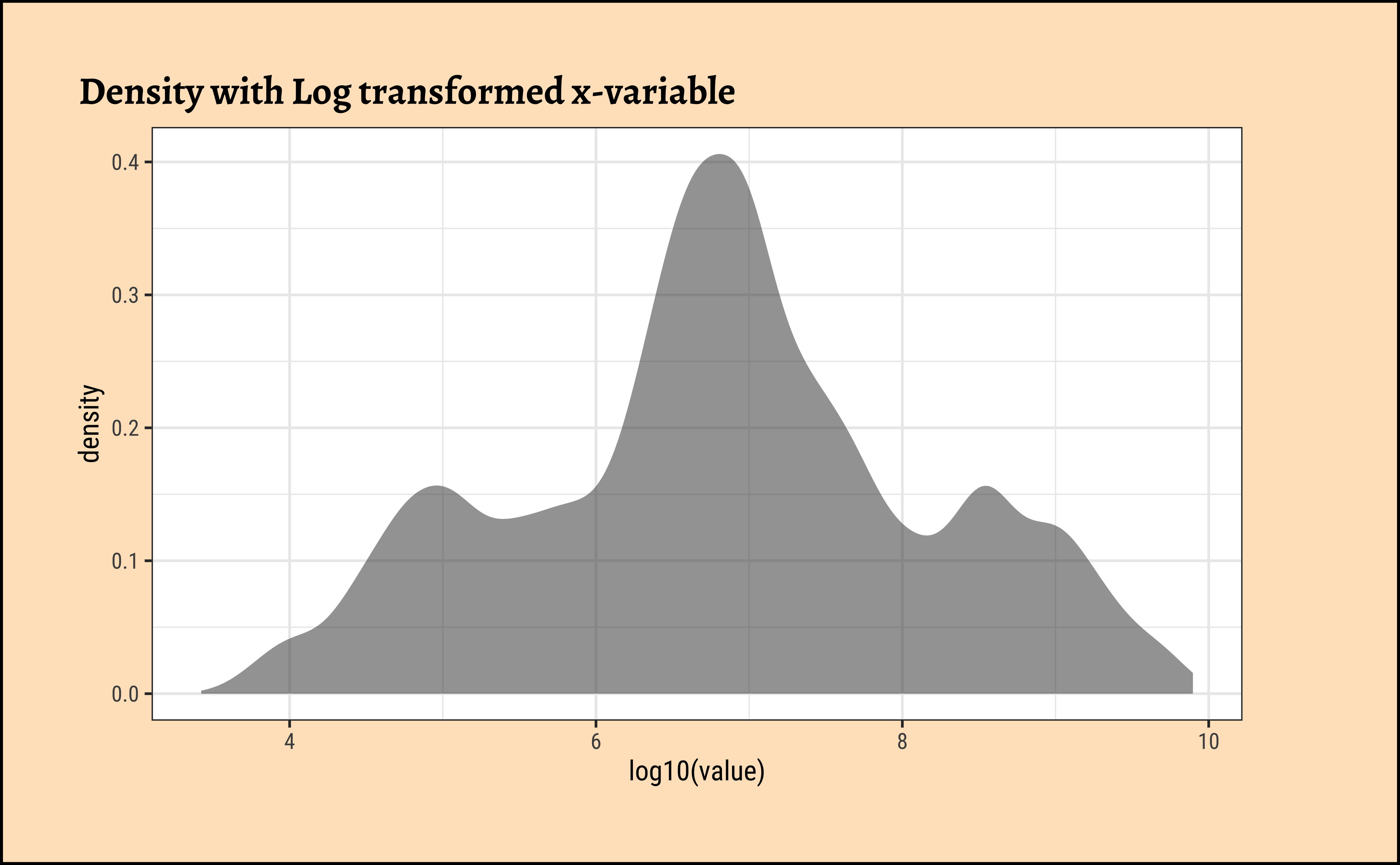
Transforming the Variable
To develop better insights with this data, we should transform the variable concerned, using say a “log” transformation:
Code
Be prepared to transform your data with log or sqrt transformations when you see skewed distributions!
City Populations, Sales across product categories, Salaries, Instagram connections, number of customers vs Companies, net worth / valuation of Companies, extreme events on stock markets….all of these could have highly skewed distributions. In such a case, the standard statistics of mean/median/sd may not convey too much information. With such distributions, one additional observation on say net worth, like say Mr Gates’, will change these measures completely. (More when we discuss Sampling)
Since very large observations are indeed possible, if not highly probable, one needs to look at the result of such an observation and its impact on a situation rather than its (mere) probability. Classical statistical measures and analysis cannot apply with long-tailed distributions. More on this later in the Module on Statistical Inference, but for now, here is a video that talks in detail about fat-tailed distributions, and how one should use them and get used to them:
Code
# options(ragg.max_dim = 7000) # to avoid error in ragg device
# Build dataset with different distributions
library(hrbrthemes)
data <- data.frame(
type = c(rep("edge peak", 1000), rep("comb", 1000), rep("normal", 1000), rep("uniform", 1000), rep("bimodal", 1000), rep("skewed", 1000)),
value = c(rnorm(900), rep(3, 100), rnorm(360, sd = 0.5), rep(c(-1, -0.75, -0.5, -0.25, 0, 0.25, 0.5, 0.75), 80), rnorm(1000), runif(1000), rnorm(500, mean = -2), rnorm(500, mean = 2), abs(log(rnorm(1000))))
)
# Represent it
data %>%
ggplot(aes(x = value)) +
geom_histogram(fill = "#69b3a2", color = "#e9ecef", alpha = 0.9) +
facet_wrap(~type, scale = "free_x") +
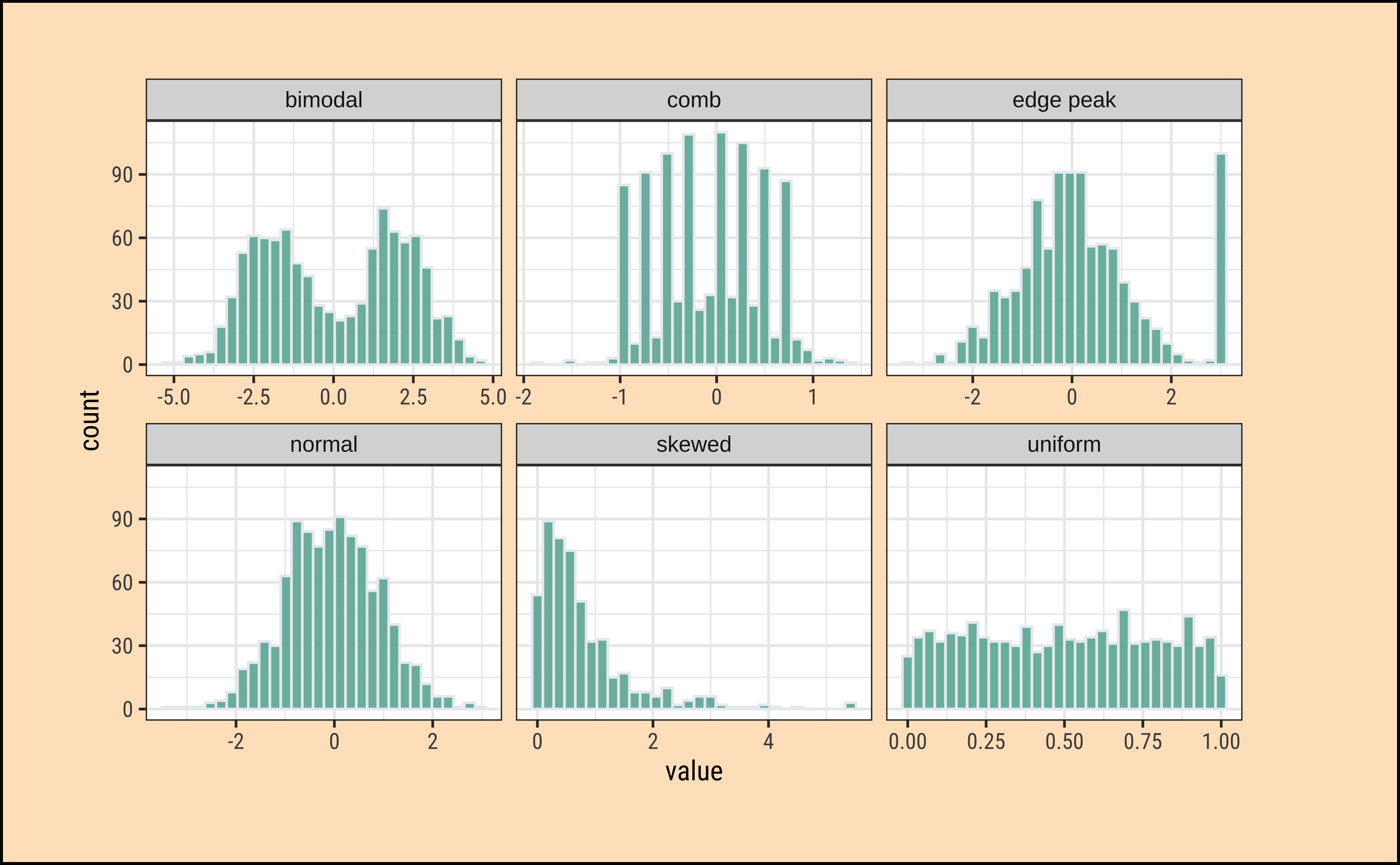
theme_custom()What insights could you develop based on these distribution shapes?
- Bimodal: Maybe two different systems or phenomena or regimes under which the data unfolds. Like the geyser dataset (. Or a machine that works differently when cold and when hot. Intermittent faulty behaviour…
- Comb: Some specific Observations occur predominantly, in an otherwise even spread or observations. In a survey many respondents round off numbers to nearest 100 or 1000. Check the distribution of the diamonds dataset for
caratvalues which are suspiciously integer numbers in too many cases.
- Edge Peak: Could even be a data entry artifact!! All unknown / unrecorded observations are recorded as \(999\) !!🙀
- Normal: Just what it says! Course Marks in a Univ cohort…
- Skewed: Income, or friends count in a set of people. Do UI/UX peasants have more followers on Insta than say CAP people?
- Uniform: The World is
notflat. Anything can happen within a range. But not much happens outside! Sharp limits…
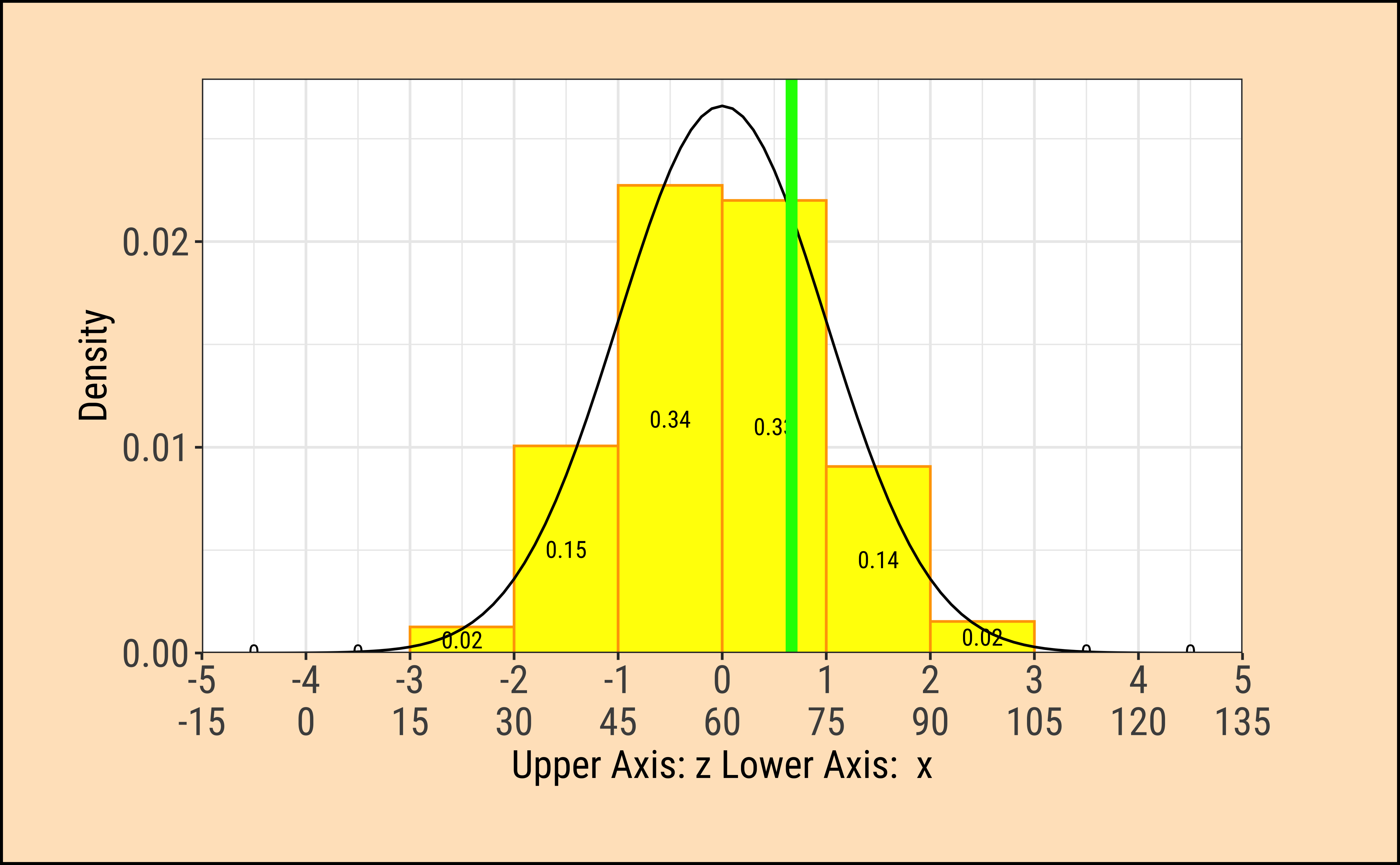
Look at the 4 graphs below:
Code
TeachHistDens(Mean = 60, Sd = 5, VLine1 = 70, AxisFontSize = 14)
TeachHistDens(Mean = 60, Sd = 15, VLine1 = 70, AxisFontSize = 14)
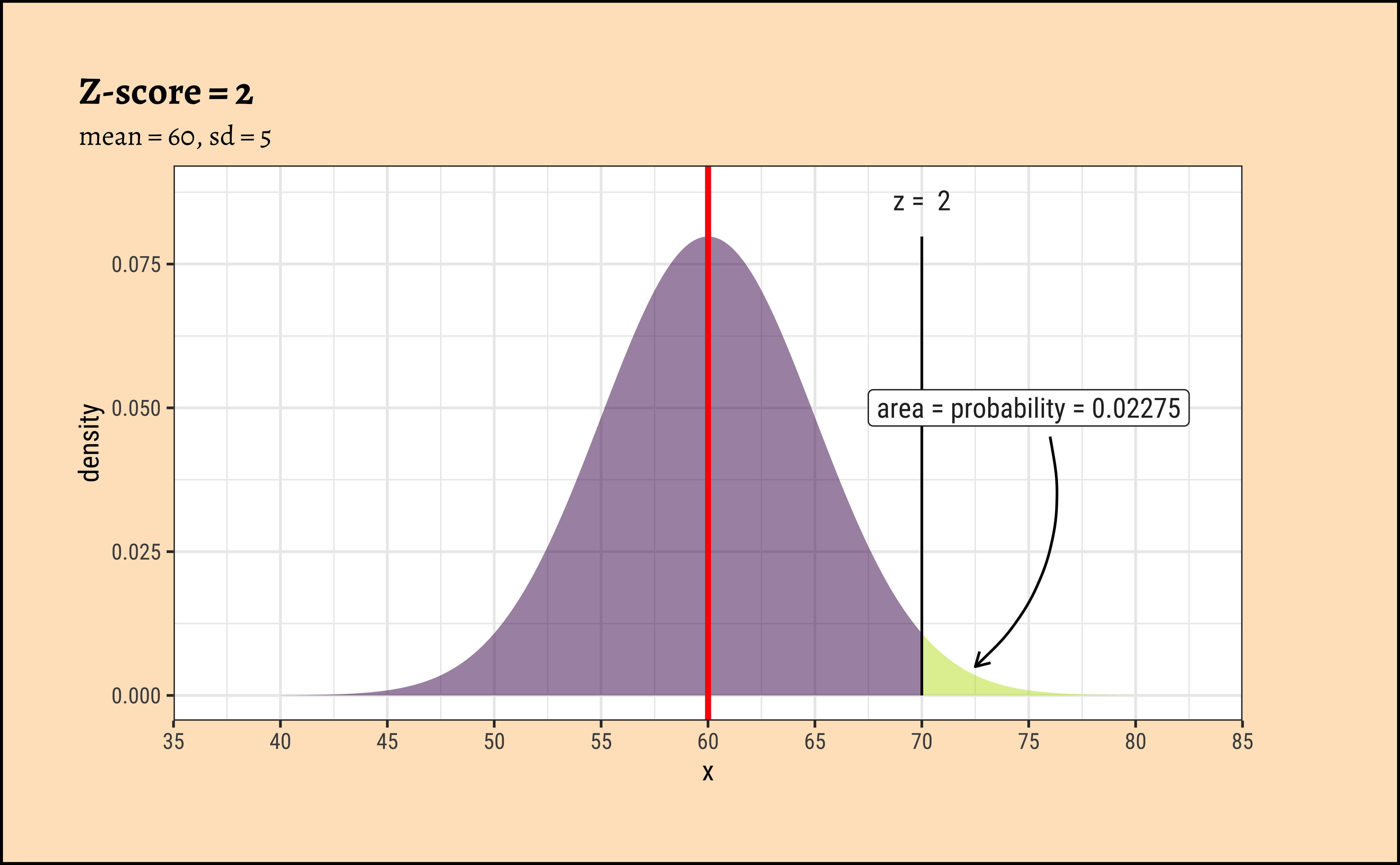
xpnorm(
mean = 60, sd = 5, q = 70, return = "plot", alpha = 0.5,
method = "gg"
) %>%
gf_vline(xintercept = 60, colour = "red", linewidth = 1) %>%
gf_annotate("label", x = 75, y = 0.05, label = "area = probability = 0.02275") %>%
gf_annotate("curve",
x = 76, y = 0.045, xend = 72.5, yend = 0.005,
curvature = -0.3, arrow = arrow(length = unit(0.2, "cm"))
) %>%
gf_labs(title = "Z-score = 2", subtitle = "mean = 60, sd = 5") %>%
gf_refine(
scale_x_continuous(
limits = c(35, 85),
breaks = seq(35, 85, by = 5),
expand = c(0, 0)
)
)
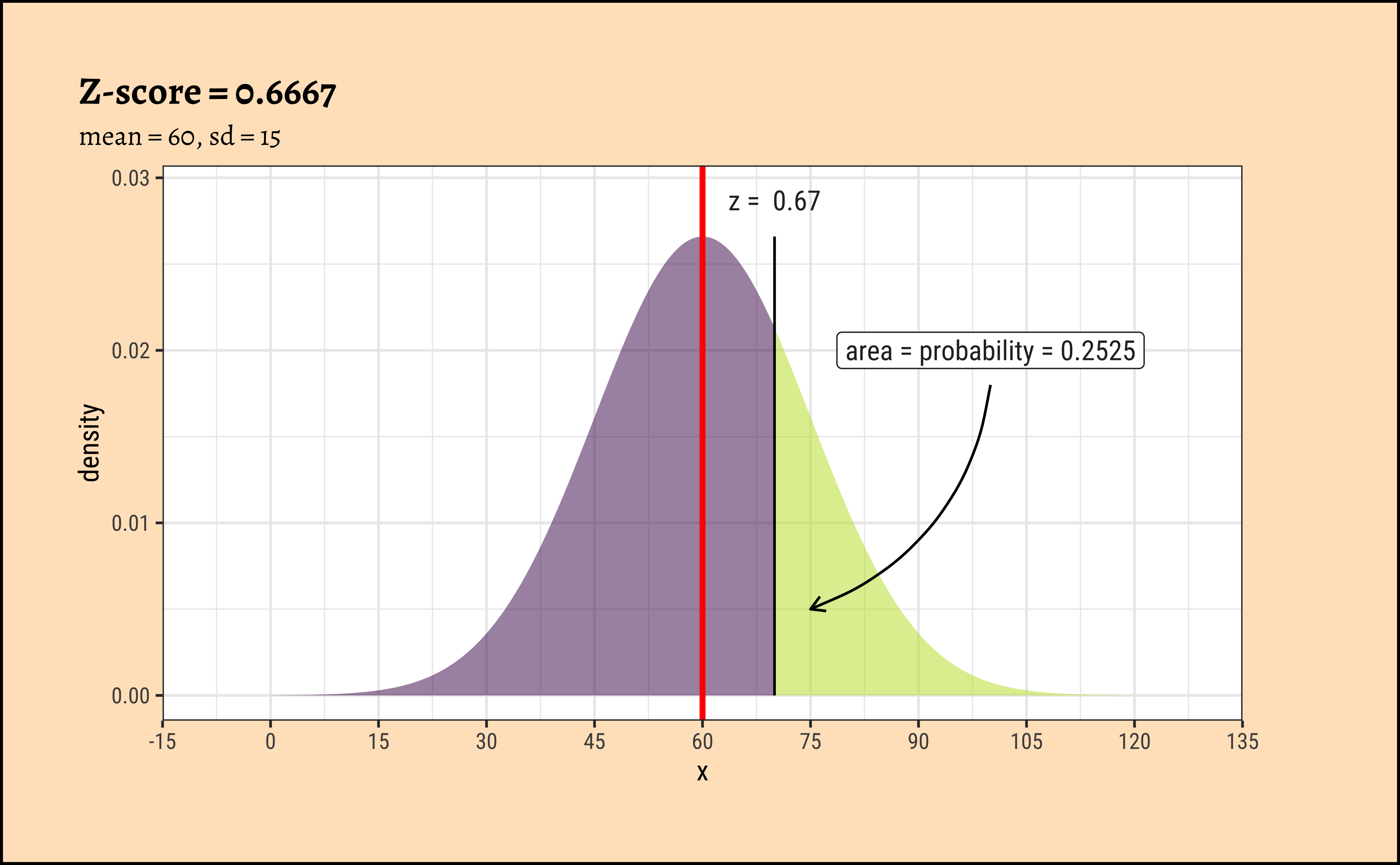
xpnorm(
mean = 60, sd = 15, q = 70, return = "plot", alpha = 0.5,
method = "gg"
) %>%
gf_vline(xintercept = 60, colour = "red", linewidth = 1) %>%
gf_annotate("label", x = 100, y = 0.02, label = "area = probability = 0.2525") %>%
gf_annotate("curve",
x = 100, y = 0.018, xend = 75, yend = 0.005,
curvature = -0.3, arrow = arrow(length = unit(0.2, "cm"))
) %>%
gf_labs(title = "Z-score = 0.6667", subtitle = "mean = 60, sd = 15") %>%
gf_refine(scale_x_continuous(
limits = c(-15, 135),
breaks = seq(-15, 135, by = 15), expand = c(0, 0)
))Understanding Z-scores
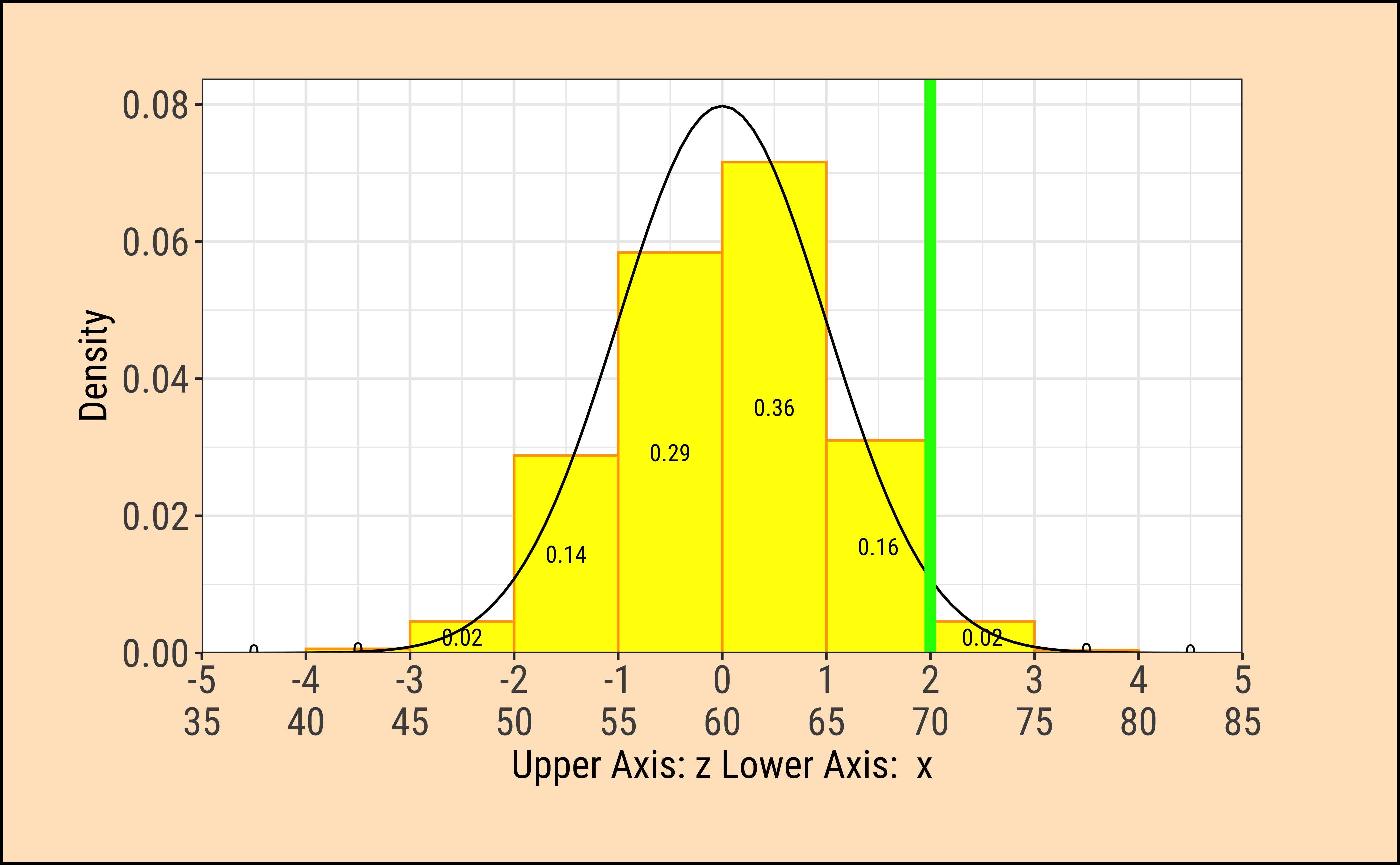
Often when we compute wish to compare distributions with different values for means and standard deviations, we resort to a scaling of the variables that are plotted in the respective distributions.
Although the densities all look the same, they are are quite different! The x-axis in each case has two scales: one is the actual value of the x-variable, and the other is the z-score which is calculated as the scaled residual from the mean:
\[ z_x = \frac{x - \mu_{x}}{\sigma_x} \tag{1}\]
where \(\mu_x\) and \(\sigma_x\) are the mean and standard deviation of the x-variable.
Important
The z-score is the distance from the mean (i.e. residual) scaled by the sd.
In the figures above, the absolute values of the random variables \(x_i\) is always \(10\) from the (identical) means \(\mu_i\). However since the \(\sigma_i\) are different, the z-score is different in each case. In the left column, the z-score is \(2\); in the right column it is \(0.6667\).
We note that the variation in density is the same at the same values of z-score.
When we make comparisons of two random variables, our comparisons are done most easily when we compare z-scores to calculate probabilities, or differences in z-scores at identical probabilities.
- Histograms are used to study the distribution of one or a few Quant variables.
- Checking the distribution of your variables one by one is probably the first task you should do when you get a new dataset.
- It delivers a good quantity of information about spread, how frequent the observations are, and if there are some outlandish ones.
- Comparing histograms side-by-side helps to provide insight about whether a Quant measurement varies with situation (a Qual variable). We will see this properly in a statistical way soon.
To complicate matters: Having said all that, the histogram is really a bar chart in disguise! You probably suspect that the “bucketing” of the Quant variable is tantamount to creating a Qual variable! Each bucket is a level in this fictitious bucketed Quant variable.
- Histograms, Frequency Distributions, and Box Plots are used for Quantitative data variables
- Histograms “dwell upon” counts, ranges, means and standard deviations
- We can split histograms on the basis of another Qualitative variable.
- Long tailed distributions need care in visualization and in inference making!
- Old Faithful Data in R (Find it!)
- Wage and Education Data from Canada
- Time taken to Open or Close Packages
Some Design Students/HCD peasants tested Elderly people, some with and some without hand pain, and observed how long they took to open or close typical packages for milk, cheese, bottles etc.
Tip
Note: reading xlsx files into R may need the the {readxl} package. Install it!!
The author illustrates these concepts through real-world examples using datasets such as diamond prices, ultramarathon race times, and global population figures. By analyzing these datasets with histograms, the author explores various aspects of data distributions, including skewness, bimodality, and the presence of outliers. The guide also introduces additional tools like the {crosstable} package and z-scores to enhance data analysis. Finally, the author encourages readers to apply these concepts to real-world datasets, developing questions and insights through the use of histograms and statistical measures.
What patterns emerge from the distributions of quantitative variables in each dataset, and what insights can we gain about the relationships between these variables?
How do different qualitative variables impact the distribution of quantitative variables in the datasets, and what are the implications of these findings for understanding the underlying phenomena?
Based on the distributions and relationships between variables, what are the most relevant questions to ask about the datasets, and what further analyses could be conducted
- Winston Chang (2024). R Graphics Cookbook. https://r-graphics.org
- See the scrolly animation for a histogram at this website: Exploring Histograms, an essay by Aran Lunzer and Amelia McNamara https://tinlizzie.org/histograms/?s=09
- Minimal R using
mosaic.https://cran.r-project.org/web/packages/mosaic/vignettes/MinimalRgg.pdf
- Sebastian Sauer, Plotting multiple plots using purrr::map and ggplot
| Package | Version | Citation |
|---|---|---|
| crosstable | 0.8.2 | Chaltiel (2025) |
| ggridges | 0.5.7 | Wilke (2025) |
| janitor | 2.2.1 | Firke (2024) |
| naniar | 1.1.0 | Tierney and Cook (2023) |
| NHANES | 2.1.0 | Pruim (2015) |
| TeachHist | 0.2.1 | Lange (2023) |
| TeachingDemos | 2.13 | Snow (2024) |
| tinytable | 0.13.0 | Arel-Bundock (2025) |
| visdat | 0.6.0 | Tierney (2017) |
| visualize | 4.5.0 | Balamuta (2023) |