Inference for a Single Mean

“The more I love humanity in general, the less I love man in particular. ― Fyodor Dostoyevsky, The Brothers Karamazov

Arvind V.

2022-11-10

…neither let us despair over how small our successes are. For however much our successes fall short of our desire, our efforts aren’t in vain when we are farther along today than yesterday.

— John Calvin

Setting up R packages

library(tidyverse)
library(mosaic)
library(ggformula)
library(infer)
library(broom) # Clean test results in tibble form
library(resampledata) # Datasets from Chihara and Hesterberg's book
library(openintro) # More datasets
library(visStatistics) # One package to rule them all
library(ggstatsplot)

Plot Fonts and Theme

Code 
library(systemfonts)
library(showtext)
## Clean the slate
systemfonts::clear_local_fonts()
systemfonts::clear_registry()
##
showtext_opts(dpi = 96) # set DPI for showtext
sysfonts::font_add(
  family = "Alegreya",
  regular = "../../../../../../fonts/Alegreya-Regular.ttf",
  bold = "../../../../../../fonts/Alegreya-Bold.ttf",
  italic = "../../../../../../fonts/Alegreya-Italic.ttf",
  bolditalic = "../../../../../../fonts/Alegreya-BoldItalic.ttf"
)

sysfonts::font_add(
  family = "Roboto Condensed",
  regular = "../../../../../../fonts/RobotoCondensed-Regular.ttf",
  bold = "../../../../../../fonts/RobotoCondensed-Bold.ttf",
  italic = "../../../../../../fonts/RobotoCondensed-Italic.ttf",
  bolditalic = "../../../../../../fonts/RobotoCondensed-BoldItalic.ttf"
)
showtext_auto(enable = TRUE) # enable showtext
##
theme_custom <- function() {
  theme_bw(base_size = 10) +

    # theme(panel.widths = unit(11, "cm"),
    #       panel.heights = unit(6.79, "cm")) + # Golden Ratio

    theme(
      plot.margin = margin_auto(t = 1, r = 2, b = 1, l = 1, unit = "cm"),
      plot.background = element_rect(
        fill = "bisque",
        colour = "black",
        linewidth = 1
      )
    ) +

    theme_sub_axis(
      title = element_text(
        family = "Roboto Condensed",
        size = 10
      ),
      text = element_text(
        family = "Roboto Condensed",
        size = 8
      )
    ) +

    theme_sub_legend(
      text = element_text(
        family = "Roboto Condensed",
        size = 6
      ),
      title = element_text(
        family = "Alegreya",
        size = 8
      )
    ) +

    theme_sub_plot(
      title = element_text(
        family = "Alegreya",
        size = 14, face = "bold"
      ),
      title.position = "plot",
      subtitle = element_text(
        family = "Alegreya",
        size = 10
      ),
      caption = element_text(
        family = "Alegreya",
        size = 6
      ),
      caption.position = "plot"
    )
}

## Use available fonts in ggplot text geoms too!
ggplot2::update_geom_defaults(geom = "text", new = list(
  family = "Roboto Condensed",
  face = "plain",
  size = 3.5,
  color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "label", new = list(
  family = "Roboto Condensed",
  face = "plain",
  size = 3.5,
  color = "#2b2b2b"
))

ggplot2::update_geom_defaults(geom = "marquee", new = list(
  family = "Roboto Condensed",
  face = "plain",
  size = 3.5,
  color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "text_repel", new = list(
  family = "Roboto Condensed",
  face = "plain",
  size = 3.5,
  color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "label_repel", new = list(
  family = "Roboto Condensed",
  face = "plain",
  size = 3.5,
  color = "#2b2b2b"
))

## Set the theme
ggplot2::theme_set(new = theme_custom())

## tinytable options
options("tinytable_tt_digits" = 2)
options("tinytable_format_num_fmt" = "significant_cell")
options(tinytable_html_mathjax = TRUE)


## Set defaults for flextable
flextable::set_flextable_defaults(font.family = "Roboto Condensed")

Introduction

In this module, we will answer a basic Question: What is the mean \(\mu\) of the population?

Recall that the mean is the first of our Summary Statistics. We wish to know more about the mean of the population from which we have drawn our data sample.

We will do this is in several ways, based on the assumptions we are willing to adopt about our data. First we will use a toy dataset with one “imaginary” sample, normally distributed and made up of 50 observations. Since we “know the answer” we will be able to build up some belief in the tests and procedures, which we will dig into to form our intuitions.

We will then use a real-world dataset to make inferences on the means of Quant variables therein, and decide what that could tell us.

Statistical Inference is almost an Attitude!

As we will notice, the process of Statistical Inference is an attitude: ain’t nothing happenin’! We look at data that we might have received or collected ourselves, and look at it with this attitude, seemingly, of some disbelief. Here is how we proceed:

  1. We state our belief that:

    • there is really nothing happening with our Research Question, and there is no reason to believe in it;
    • the sample is just one of many, and the value/statistic indicated by the sample is the outcome of random chance (NULL Belief / Hypothesis).

  2. We then calculate how slim the chances (Relative Probability! Remember we are Frequentists!) are of the given data sample / statistic showing up like that, given our NULL belief. It is a distance measurement of sorts, literally embodying the idea of far-fetched-ness!!

  3. If the chances of the sample are too low, then that might alter our belief. This is the attitude that lies at the heart of Null Hypothesis Significance Testing (NHST).

Important

The calculation of chances is both a logical, and a possible procedure since we are dealing with samples from a population, and imagining a distribution of sample statistics. If many other samples give us quite different statistics, then we would discredit the one we derive from it.

Each test we perform will mechanize this attitude in different ways, based on assumptions and conveniences. (And history)

Case Study #1: Toy data

Since the CLT assumes the sample is normally-distributed, let us generate a sample that is just so:

set.seed(42) # for replication
#
# Data as individual vectors
# ( for t.tests etc)
# Generate normally distributed data with mean = 2, sd = 2, length = 50
y <- rnorm(n = 50, mean = 2, sd = 2)

# And as tibble too
mydata <- tibble(y = y)
mydata

Inspecting and Charting Data

## Set Plot theme
ggplot2::theme_set(new = theme_custom())

mydata %>%
  gf_density(~y) %>%
  gf_fitdistr(dist = "dnorm") %>%
  gf_labs(
    title = "Densities of Original Data Variables",
    subtitle = "Compared with Normal Density"
  )
Figure 1: Toy Data Distribution

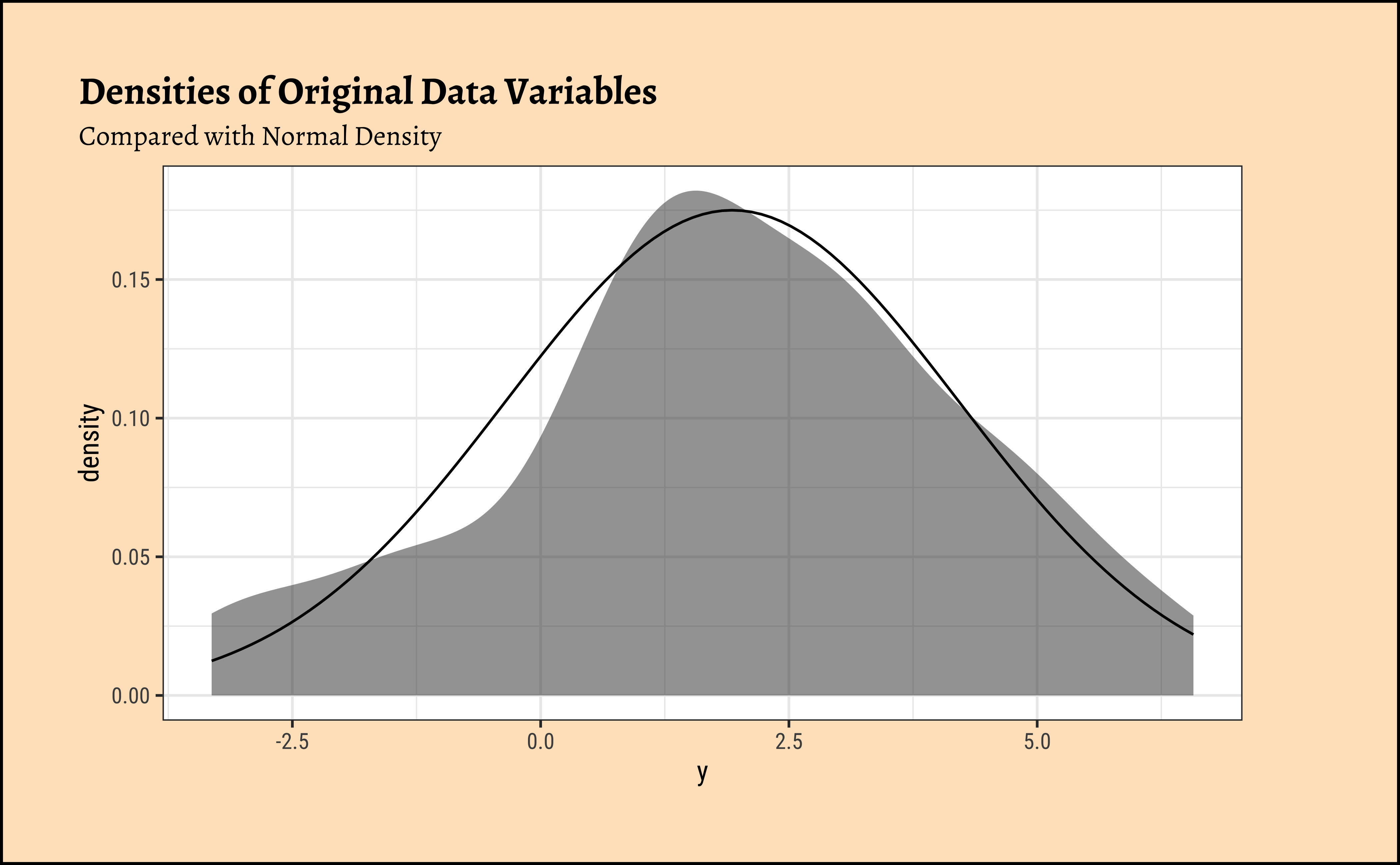
Observations from Density Plots

  • The variable \(y\) appear to be centred around
  • It does not seem to be normally distributed…
  • So assumptions are not always valid…

Research Question

Research Questions are always about the population! Here goes:

Research Question

Could the mean of the population \(\mu\), from which the sample y has been drawn, be \(0\)?

Assumptions

Testing for Normality

The y-variable does not appear to be normally distributed. This would affect the test we can use to make inferences about the population mean.
There are formal tests for normality too. We will do them in the next case study. For now, let us proceed naively.

Inference

A. Model

We have \(mean(y) = \bar{y}.\) We formulate “our disbelief” of \(\bar{y}\) with a NULL Hypothesis, about the population as follows:

\[ \ H_0: \mu = 0 \] And the alternative hypothesis, again about the population as

\[ H_a:\mu \ne 0 \]

B. Code

# t-test
t1 <- mosaic::t_test(
  y, # Name of variable
  mu = 0, # belief of population mean
  alternative = "two.sided"
) %>% # Check both sides

  broom::tidy() # Make results presentable, and plottable!!
t1

So \(\bar{y}\) i.e. the estimate is \(2.045689\). The confidence intervals do not straddle zero. The chances that this particular value of mean (\(2.045689\)) would randomly occur under the assumption that \(\mu\) is zero, are exceedingly slim, \(p.value = 1.425 * 10^{-8}\). Hence we can reject the NULL hypothesis that the true population, of which y is a sample, could have mean \(\mu = 0\).

“Signed Rank” Values: A Small Digression

When the Quant variable we want to test for is not normally distributed, we need to think of other ways to perform our inference. Our assumption about normality has been invalidated.
Most statistical tests use the actual values of the data variables. However, in these cases where assumptions are invalidated, the data are used in rank-transformed sense/order. In some cases the signed-rank of the data values is used instead of the data itself. The signed ranks are then tested to see if there are more of one polarity than the other, roughly speaking, and how probable this could be.

Signed Rank is calculated as follows:

  1. Take the absolute value of each observation in a sample
  2. Place the ranks in order of (absolute magnitude). The smallest number has rank = 1 and so on.
  3. Give each of the ranks the sign of the original observation ( + or -)
signed_rank <- function(x) {
  sign(x) * rank(abs(x))
}

Since we are dealing with the mean, the sign of the rank becomes important to use.

A. Model

\[ mean(signed\_rank(y)) = \beta_0 \]

\[ H_0: \beta_0 = 0 \] \[ H_a: \beta_0 \ne 0 \]

B. Code

# Standard Wilcoxon Signed_Rank Test
t2 <- wilcox.test(y, # variable name
  mu = 0, # belief
  alternative = "two.sided",
  conf.int = TRUE,
  conf.level = 0.95
) %>%
  broom::tidy()
t2
# Can also do this equivalently
# t-test with signed_rank data
t3 <- t.test(signed_rank(y),
  mu = 0,
  alternative = "two.sided",
  conf.int = TRUE,
  conf.level = 0.95
) %>%
  broom::tidy()
t3

Again, the confidence intervals do not straddle \(0\), and we need to reject the belief that the mean is close to zero.

Note

Note how the Wilcoxon Test reports results about \(y\), even though it computes with \(signed-rank(y)\). The “equivalent t-test” used with signed-rank data cannot do this, since it uses “rank” data as-is.

We saw from the diagram created by Allen Downey that there is only one test 1! We will now use this philosophy to develop a technique that allows us to mechanize several Statistical Models in that way, with nearly identical code.

We can use two packages in R, mosaic to develop our intuition for what are called permutation based statistical tests; and a more recent package called infer in R which can do pretty much all of this, including visualization.

We will stick with mosaic for now. We will do a permutation test first, and then a bootstrap test. In subsequent modules, we will use infer also.

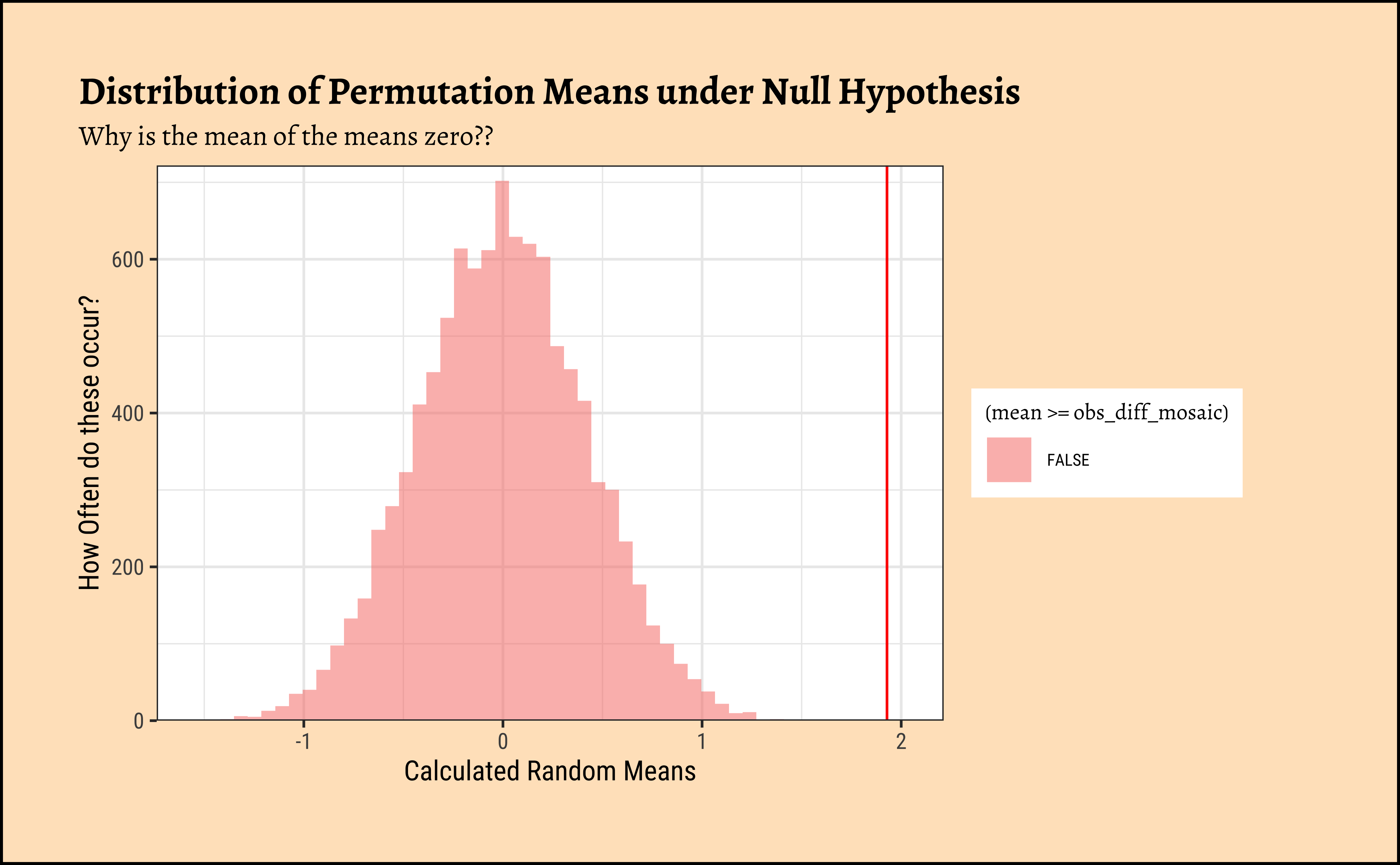
For the Permutation test, we mechanize our belief that \(\mu = 0\) by shuffling the polarities of the y observations randomly 4999 times to generate other samples from the population \(y\) could have come from2. If these samples can frequently achieve \(\bar{y_i} \leq 0\), then we might believe that the population mean may be 0!

We see that the means here that chances that the randomly generated means can exceed our real-world mean are about \(0\)! So the mean is definitely different from \(0\).

Code 
ggplot2::theme_set(new = theme_custom())

# Calculate exact mean
obs_mean <- mean(~y, data = mydata)
belief1 <- 0 # What we think the mean is
obs_diff_mosaic <- obs_mean - belief1
obs_diff_mosaic
## Steps in Permutation Test
## Repeatedly Shuffle polarities of data observations
## Take means
## Compare all means with the real-world observed one
null_dist_mosaic <-
  mosaic::do(9999) * mean(
    ~ abs(y) *
      sample(c(-1, 1), # +/- 1s multiply y
        length(y), # How many +/- 1s?
        replace = T
      ), # select with replacement
    data = mydata
  )
##
range(null_dist_mosaic$mean)
##
## Plot this NULL distribution
gf_histogram(
  ~mean,
  data = null_dist_mosaic,
  fill = ~ (mean >= obs_diff_mosaic),
  bins = 50, title = "Distribution of Permutation Means under Null Hypothesis",
  subtitle = "Why is the mean of the means zero??"
) %>%
  gf_labs(
    x = "Calculated Random Means",
    y = "How Often do these occur?"
  ) %>%
  gf_vline(xintercept = obs_diff_mosaic, colour = "red") %>%
  gf_refine(
    scale_y_continuous(expand = expansion(add = c(0, 20))),
    scale_x_continuous(expand = expansion(add = c(0.25, 0.25)))
  )

# p-value
# Null distributions are always centered around zero. Why?
prop(~ mean >= obs_diff_mosaic,
  data = null_dist_mosaic
)
[1] 1.928656
[1] -1.454320  1.516059
prop_TRUE 
        0
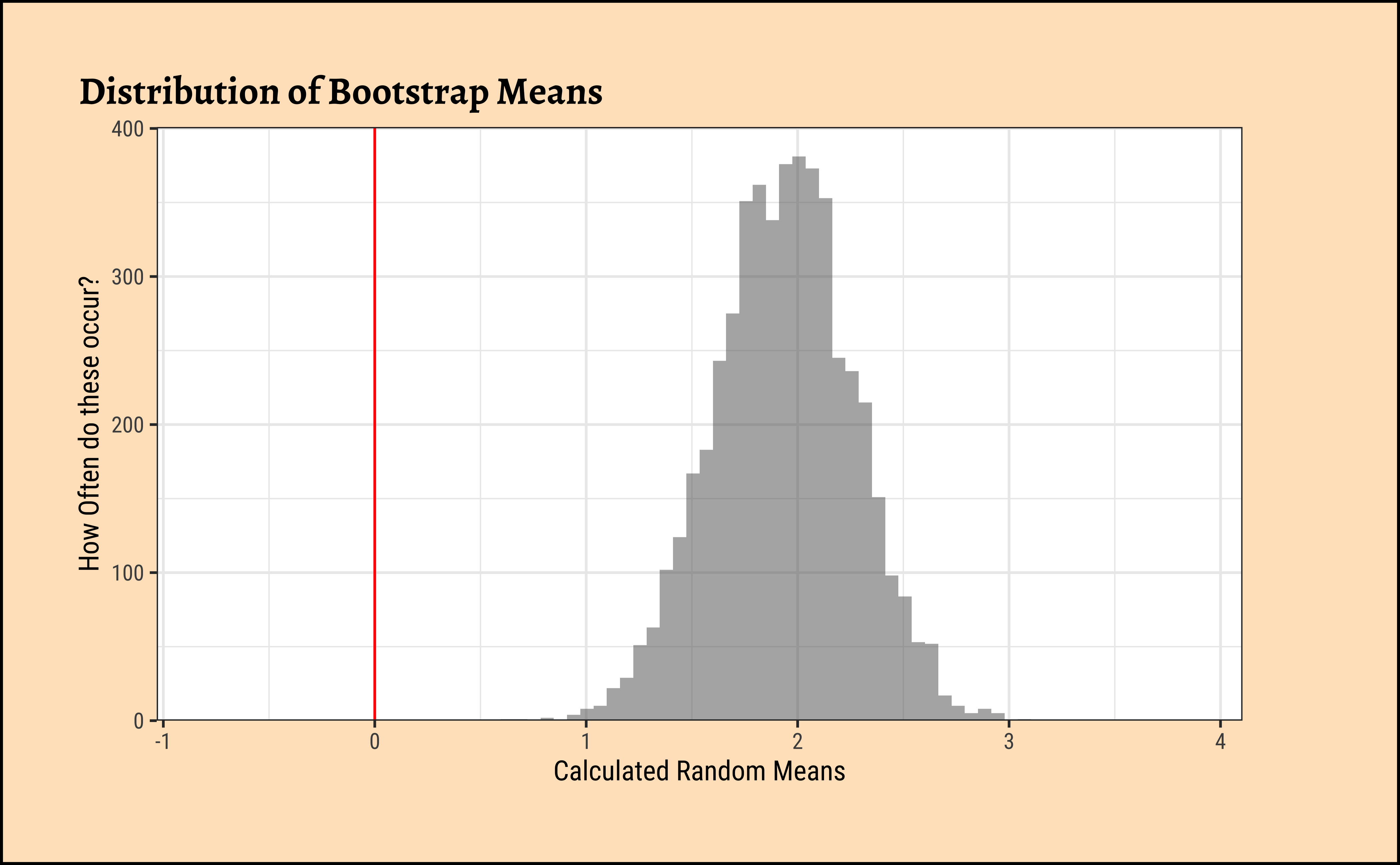
Figure 2: Permutation Test for One Mean

Let us try the bootstrap test now: Here we simulate samples, similar to the one at hand, using repeated sampling the sample itself, with replacement, a process known as bootstrapping, or bootstrap sampling.

Code 
ggplot2::theme_set(new = theme_custom())

## Resample with replacement from the one sample of 50
## Calculate the mean each time
null_toy_bs <- mosaic::do(4999) *
  mean(
    ~ sample(y,
      replace = T
    ), # select with replacement
    data = mydata
  )

## Plot this NULL distribution
gf_histogram(
  ~mean,
  data = null_toy_bs,
  bins = 50,
  title = "Distribution of Bootstrap Means"
) %>%
  gf_labs(
    x = "Calculated Random Means",
    y = "How Often do these occur?"
  ) %>%
  gf_vline(xintercept = ~belief1, colour = "red") %>%
  gf_refine(
    scale_y_continuous(expand = expansion(add = c(0, 20))),
    scale_x_continuous(expand = expansion(add = c(1, 1)))
  )

prop(~ mean >= belief1,
  data = null_toy_bs
) +
  prop(~ mean <= -belief1,
    data = null_toy_bs
  )
prop_TRUE 
        1
Figure 3: Bootstrap Test for One Mean

Permutation vs Bootstrap

There is a difference between the two. The bootstrap test uses the sample at hand to generate many similar samples without access to the population, and calculates the statistic needed (i.e. mean). No Hypothesis is stated. The distribution of bootstrap samples looks “similar” to that we might obtain by repeatedly sampling the population itself. (centred around a population parameter, i.e. \(\mu\))

The permutation test generates many permutations of the data and generates appropriates measures/statistics under the NULL hypothesis. Which is why the permutation test has a NULL distribution centered at \(0\) in this case, our NULL hypothesis.

As student Sneha Manu Jacob remarked in class, Permutation flips the signs of the data values in our sample; Bootstrap flips the number of times each data value is (re)used. Good Insight!!

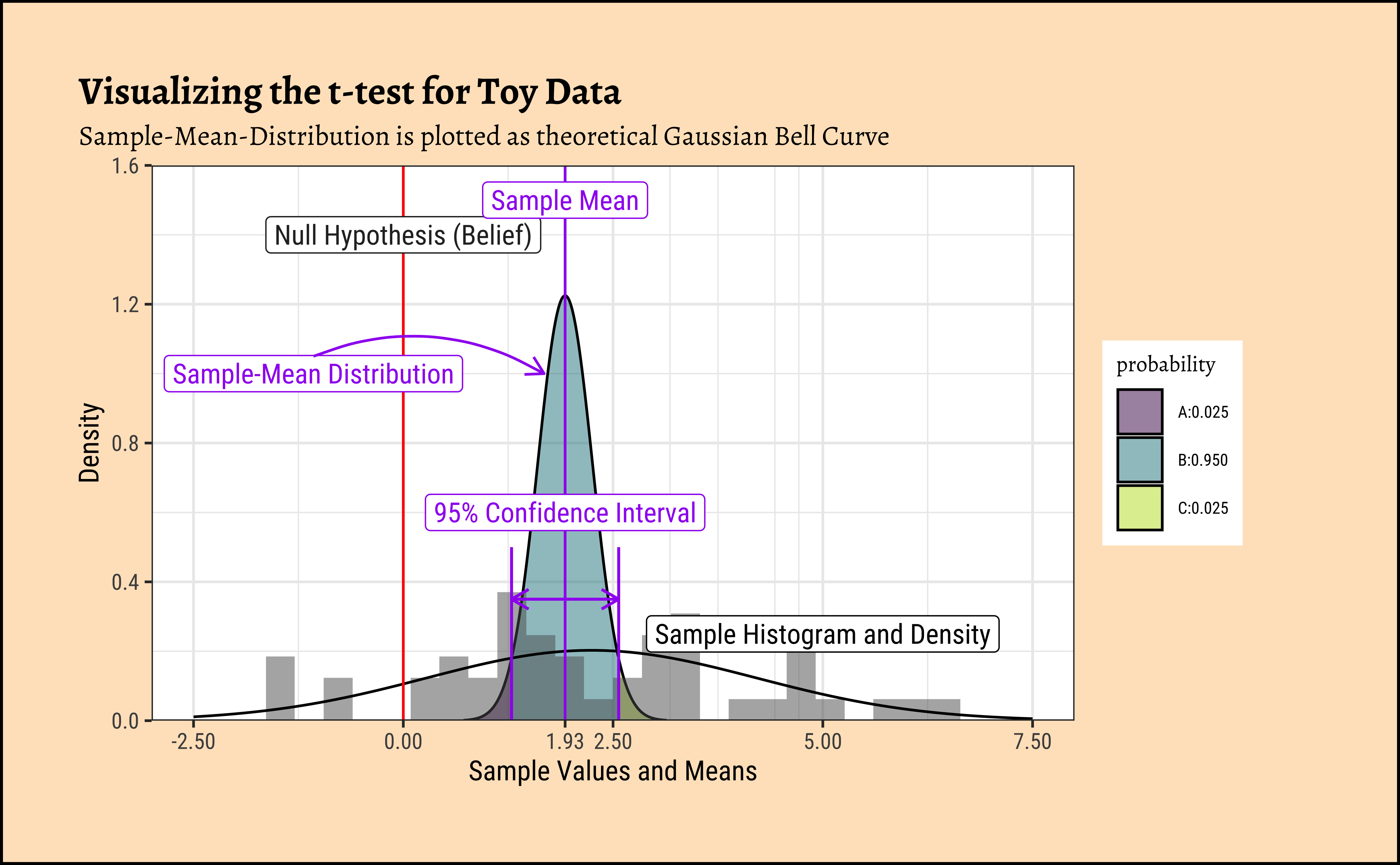
Yes, the t-test works, but what is really happening under the hood of the t-test? The inner mechanism of the t-test can be stated in the following steps:

  1. Calculate the mean of the sample \(\bar{y}\).
  2. Calculate the sd of the sample, and, assuming the sample is normally distributed, calculate the standard error (i.e. \(\frac{sd}{\sqrt{n}}\))
  3. Take the difference between the sample mean \(\bar{y}\) and our expected/believed population mean \(\mu\).
  4. Scale the difference by the standard error to get a test statistic \(t\).
  5. If the test statistic is more than \(\pm 1.96\), we can say that it is beyond the the confidence interval of the sample mean \(\bar{y}\).
  6. Therefore if the difference between actual and believed is far beyond the confidence interval, hmm…we cannot think our belief is correct and we change our opinion.

Let us translate that mouthful into calculations!

(mean_belief_pop <- 0.0) # Assert our belief
(std_error <- sd(y) / sqrt(length(y)))
(mean_y <- mean(y))
(conf_int <- tibble(ci_low = mean_y - 1.96 * std_error, ci_high = mean_y + 1.96 * std_error))
(t <- (mean_y - mean_belief_pop) / std_error)
[1] 0

Null Hypothesis / Belief

[1] 0.3256867

Standard Error

[1] 1.928656

Sample Mean

Confidence Intervals

[1] 5.921815

Test Statistic

How can we visualize this?

Code 
ggplot2::theme_set(new = theme_custom())

mosaic::xqnorm(
  p = c(0.025, 0.975), mean = sample_mean, sd = sample_se,
  return = c("value"), verbose = T, plot = F
) -> xq

## Sample-Mean Distribution
xqnorm(
  p = c(0.025, 0.975), mean = sample_mean, sd = sample_se,
  digits = 3, plot = TRUE,
  return = c("plot"), verbose = F, alpha = 0.5, colour = "black",
  system = "gg"
) %>%
  gf_dhistogram(~y, data = mydata, inherit = F) %>%
  gf_fitdistr(~y, data = mydata) %>%
  gf_vline(xintercept = ~mean_belief_pop, colour = "red") %>%
  gf_vline(xintercept = sample_mean, colour = "purple") %>%
  ## Sample Distribution
  gf_annotate(
    geom = "label", x = 5, y = 0.25,
    label = "Sample Histogram and Density",
    colour = "black"
  ) %>%
  ## Null Hypothesis
  gf_annotate(
    geom = "label", x = mean_belief_pop, y = 1.4,
    label = "Null Hypothesis (Belief)"
  ) %>%
  ## Sampling Mean Distribution
  gf_annotate(
    geom = "label", x = sample_mean - 3, y = 1.0,
    label = "Sample-Mean Distribution", colour = "purple"
  ) %>%
  gf_annotate("curve",
    x = sample_mean - 3, y = 1.05,
    xend = sample_mean - 0.25, yend = 1.0,
    curvature = -0.25, color = "purple",
    arrow = arrow(length = unit(0.25, "cm"))
  ) %>%
  ## Observed Mean
  gf_annotate(
    geom = "label", x = sample_mean, y = 1.5,
    label = "Sample Mean", colour = "purple"
  ) %>%
  ## Confidence Intervals
  gf_annotate(
    geom = "label", x = sample_mean, y = 0.6,
    label = "95% Confidence Interval",
    colour = "purple"
  ) %>%
  gf_annotate("segment",
    x = xq[1], y = 0.0,
    xend = xq[1], yend = 0.5,
    color = "purple", linewidth = 0.5
  ) %>%
  gf_annotate("segment",
    x = xq[2], y = 0.0,
    xend = xq[2], yend = 0.5,
    color = "purple", linewidth = 0.5
  ) %>%
  gf_annotate("segment",
    x = xq[1], y = 0.35,
    xend = xq[2], yend = 0.35,
    color = "purple", linewidth = 0.5,
    arrow = arrow(length = unit(0.25, "cm"), ends = "both")
  ) %>%
  gf_labs(
    title = "Visualizing the t-test for Toy Data",
    subtitle = "Sample-Mean-Distribution is plotted as theoretical Gaussian Bell Curve",
    x = "Sample Values and Means", y = "Density"
  ) %>%
  gf_refine(
    scale_y_continuous(limits = c(0, 1.6), expand = c(0, 0)),
    scale_x_continuous(
      limits = c(-2.5, 7.5),
      breaks = c(-2.5, 0, 2.5, 5, 7.5, sample_mean),
      labels = scales::number_format(
        accuracy = 0.01,
        decimal.mark = "."
      )
    )
  ) %>%
  gf_theme(theme_custom())
Figure 4: Visualizing the t-test for Toy Data

We see that the difference between means is 5.9218152 times the std_error! At a distance of \(1.96\) (either way) the probability of this data happening by chance already drops to \(2.5 \%\) !! At this distance of 5.9218152, we would have negligible probability of this data occurring by chance!

Case Study #2: Exam data

Let us now choose a dataset from the openintro package:

data("exam_grades", package = "openintro")
exam_grades

Research Question

There are quite a few Quant variables in the data. Let us choose course_grade as our variable of interest. What might we wish to find out?

Research Question

In general, the Teacher in this class is overly generous with grades unlike others we know, and so the average course-grade is equal to 80% !!

Inspecting and Charting Data

ggplot2::theme_set(new = theme_custom())

exam_grades %>%
  gf_density(~course_grade) %>%
  gf_fitdistr(dist = "dnorm") %>%
  gf_labs(
    title = "Density of Course Grade",
    subtitle = "Compared with Normal Density"
  )
Figure 5: Exam Grades Distribution

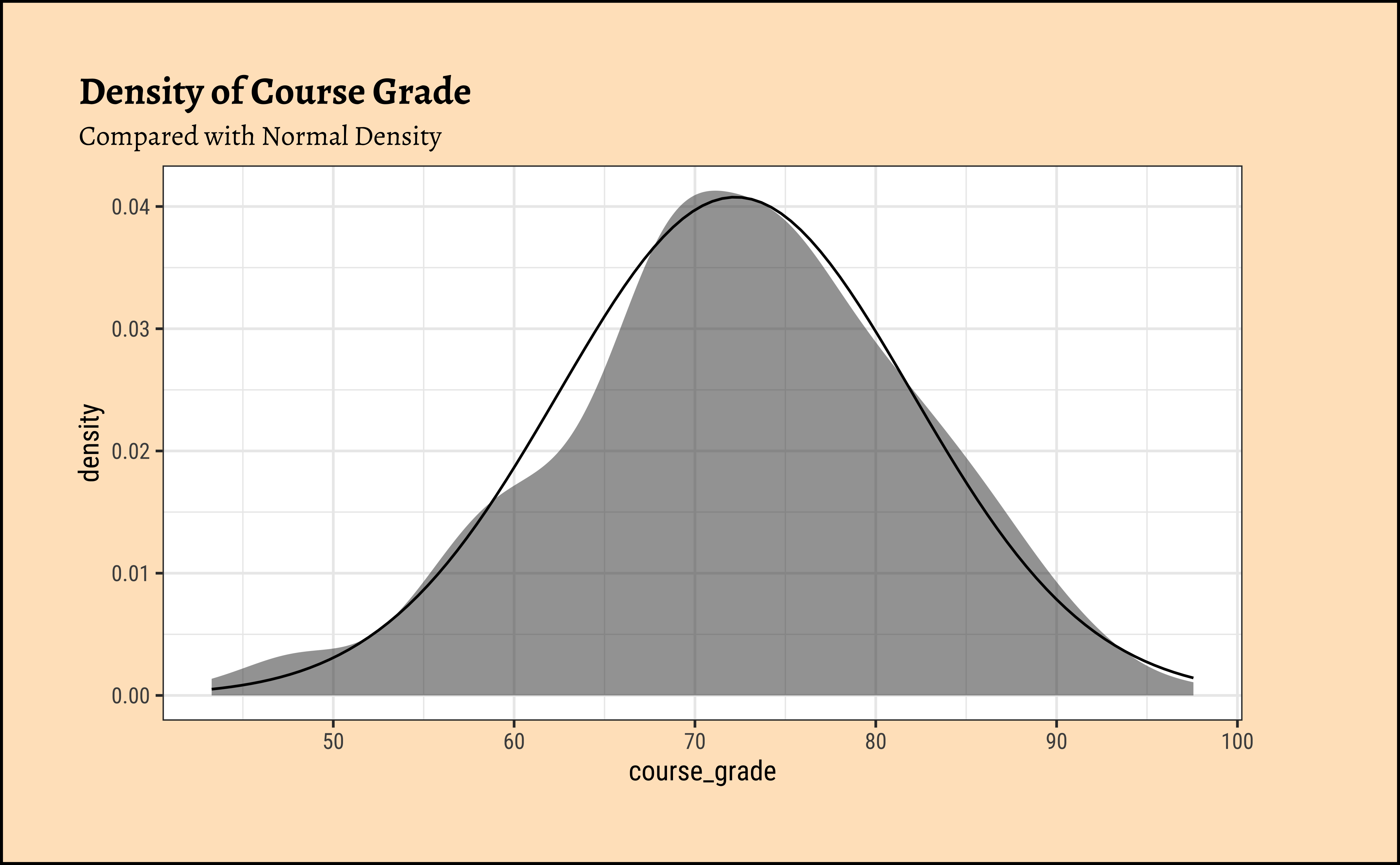
Hmm…data looks normally distributed. But this time we will not merely trust our eyes, but do a test for it.

Testing Assumptions in the Data

Is the data normally distributed?

stats::shapiro.test(x = exam_grades$course_grade) %>%
  broom::tidy()

The Shapiro-Wilks Test tests whether a data variable is normally distributed or not. Without digging into the maths of it, let us say it makes the assumption that the variable is so distributed and then computes the probability of how likely this is. So a high p-value (\(0.47\)) is a good thing here.

When we have large Quant variables ( i.e. with length >= 5000), the function shapiro.test does not work, and we use an Anderson-Darling1 test to confirm normality:

library(nortest)
# Especially when we have >= 5000 observations
nortest::ad.test(x = exam_grades$course_grade) %>%
  broom::tidy()

So course_grade is a normally-distributed variable. There are no exceptional students! Hmph! Peasants.

Inference

A. Model

We have that \(mean(course\_grade) = \beta_0\). As before, we formulate “our (dis)belief” in this sample mean with a NULL Hypothesis about the population, as follows:

\[ \ H_0: \mu= 80 \]

\[ H_a: \mu \ne 80 \]

B. Code

# t-test
t4 <- mosaic::t_test(
  exam_grades$course_grade, # Name of variable
  mu = 80, # belief
  alternative = "two.sided"
) %>% # Check both sides
  broom::tidy()
t4

So, we can reject the NULL Hypothesis that the average grade in the population of students who have taken this class is 80, since there is a minuscule chance that we would see an observed sample mean of 72.238, if the population mean \(\mu\) had really been \(80\).

# t-test
t5 <- wilcox.test(
  exam_grades$course_grade, # Name of variable
  mu = 90, # belief
  alternative = "two.sided",
  conf.int = TRUE,
  conf.level = 0.95
) %>% # Check both sides

  broom::tidy() # Make results presentable, and plottable!!
t5

This test too suggests that the average course grade is different from 80.

Why compare on both sides?

Note that we have computed whether the average course_grade is generally different from 80 for this Teacher. We could have computed whether it is greater, or lesser than 80 ( or any other number too). Read this article for why it is better to do a “two.sided” test in most cases.

Code 
ggplot2::theme_set(new = theme_custom())

# Calculate exact mean
obs_mean_grade <- mean(~course_grade, data = exam_grades)
belief <- 80
obs_grade_diff <- belief - obs_mean_grade
## Steps in a Permutation Test
## Repeatedly Shuffle polarities of data observations
## Take means
## Compare all means with the real-world observed one
null_dist_grade <-
  mosaic::do(4999) *
    mean(
      ~ (course_grade - belief) *
        sample(c(-1, 1), # +/- 1s multiply y
          length(course_grade), # How many +/- 1s?
          replace = T
        ), # select with replacement
      data = exam_grades
    )

## Plot this NULL distribution
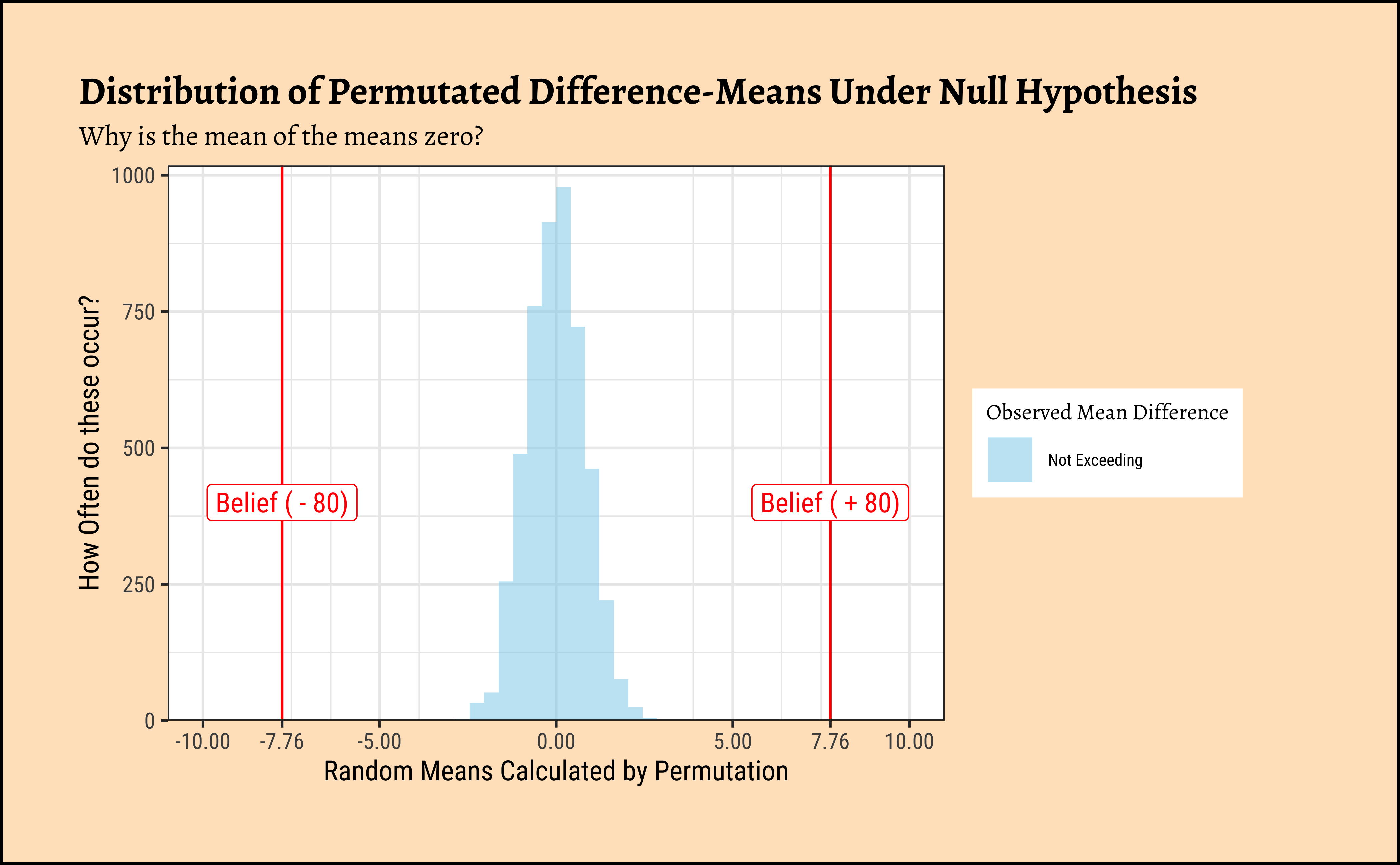
gf_histogram(
  ~mean,
  data = null_dist_grade,
  fill = ~ (mean >= obs_grade_diff),
  bins = 50,
  title = "Distribution of Permutated Difference-Means Under Null Hypothesis",
  subtitle = "Why is the mean of the means zero?"
) %>%
  gf_labs(
    x = "Random Means Calculated by Permutation",
    y = "How Often do these occur?"
  ) %>%
  gf_vline(xintercept = obs_grade_diff, colour = "red") %>%
  gf_vline(xintercept = -obs_grade_diff, colour = "red") %>%
  gf_annotate(
    geom = "label", x = obs_grade_diff, y = 400,
    label = "Belief ( + 80)",
    colour = "red"
  ) %>%
  gf_annotate(
    geom = "label", x = -obs_grade_diff, y = 400,
    label = "Belief ( - 80)",
    colour = "red"
  ) %>%
  gf_refine(
    scale_fill_manual(
      values = c("skyblue", "grey"),
      name = "Observed Mean Difference",
      labels = c("Not Exceeding", "Exceeding")
    ),
    scale_x_continuous(
      limits = c(-10, 10),
      breaks = c(-10, -5, -obs_grade_diff, 0, obs_grade_diff, 5, 10),
      labels = scales::number_format(
        accuracy = 0.01,
        decimal.mark = "."
      )
    )
  ) %>%
  gf_refine(scale_y_continuous(expand = expansion(add = c(0, 40))))


# p-value
# Permutation distributions are always centered around zero. Why?
prop(~ mean >= obs_grade_diff,
  data = null_dist_grade
) +
  prop(~ mean <= -obs_grade_diff,
    data = null_dist_grade
  )
prop_TRUE 
        0
Figure 6: Permutation Test for One Mean

And let us now do the bootstrap test:

Code 
ggplot2::theme_set(new = theme_custom())

null_grade_bs <- mosaic::do(4999) *
  mean(
    ~ sample(course_grade,
      replace = T
    ), # select with replacement
    data = exam_grades
  )

## Plot this NULL distribution
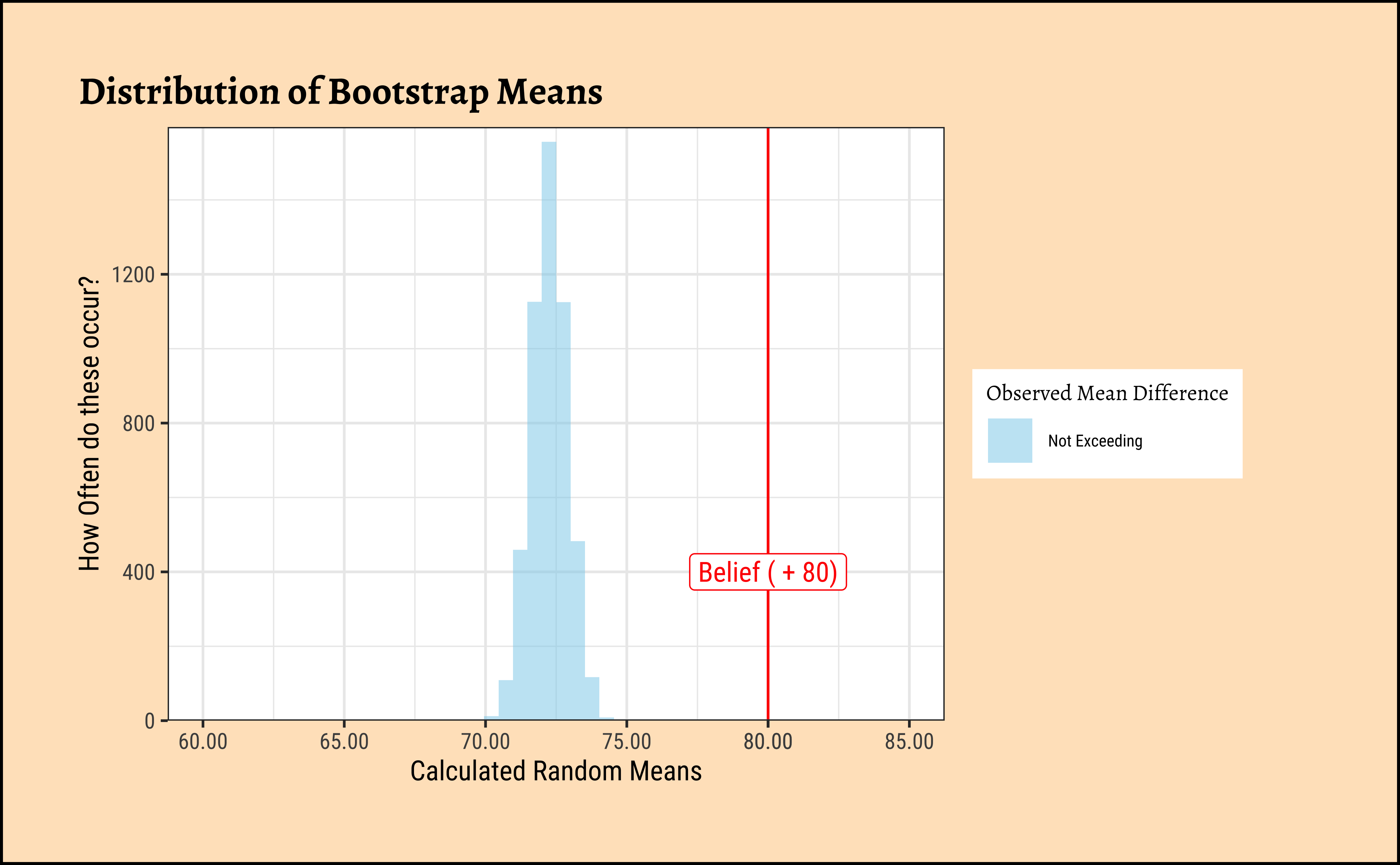
gf_histogram(
  ~mean,
  data = null_grade_bs,
  fill = ~ (mean >= obs_grade_diff),
  bins = 50,
  title = "Distribution of Bootstrap Means"
) %>%
  gf_labs(
    x = "Calculated Random Means",
    y = "How Often do these occur?"
  ) %>%
  gf_vline(xintercept = ~belief, colour = "red") %>%
  gf_annotate(
    geom = "label", x = belief, y = 400,
    label = "Belief ( + 80)",
    colour = "red"
  ) %>%
  gf_refine(
    scale_fill_manual(
      values = c("skyblue", "grey"),
      name = "Observed Mean Difference",
      labels = c("Not Exceeding", "Exceeding")
    ),
    scale_x_continuous(
      limits = c(60, 85),
      breaks = c(60, 65, 70, 75, 80, 85, belief),
      labels = scales::number_format(
        accuracy = 0.01,
        decimal.mark = "."
      )
    )
  ) %>%
  gf_refine(scale_y_continuous(expand = expansion(add = c(0, 40))))

prop(~ mean >= belief,
  data = null_grade_bs
) +
  prop(~ mean <= -belief,
    data = null_grade_bs
  )
prop_TRUE 
        0
Figure 7: Bootstrap Test for One Mean

The permutation test shows that we are not able to “generate” the believed mean-difference with any of the permutations. Likewise with the bootstrap, we are not able to hit the believed mean with any of the bootstrap samples.

Hence there is no reason to believe that the belief (80) might be a reasonable one and we reject our NULL Hypothesis that the mean is equal to 80.

Let us plot the sample distribution, the theoretical distribution of the sample mean, and the confidence intervals, as we did before for the toy data.

(obs_mean_2 <- mean(exam_grades$course_grade))
(mean_belief_pop_2 <- 80.0) # Assert our belief)
(sample_sd_2 <- sd(exam_grades$course_grade))
(sample_se_2 <- sample_sd_2 / sqrt(length(exam_grades$course_grade)))
(t_statistic_2 <- (obs_mean_2 - mean_belief_pop_2) / sample_se_2)
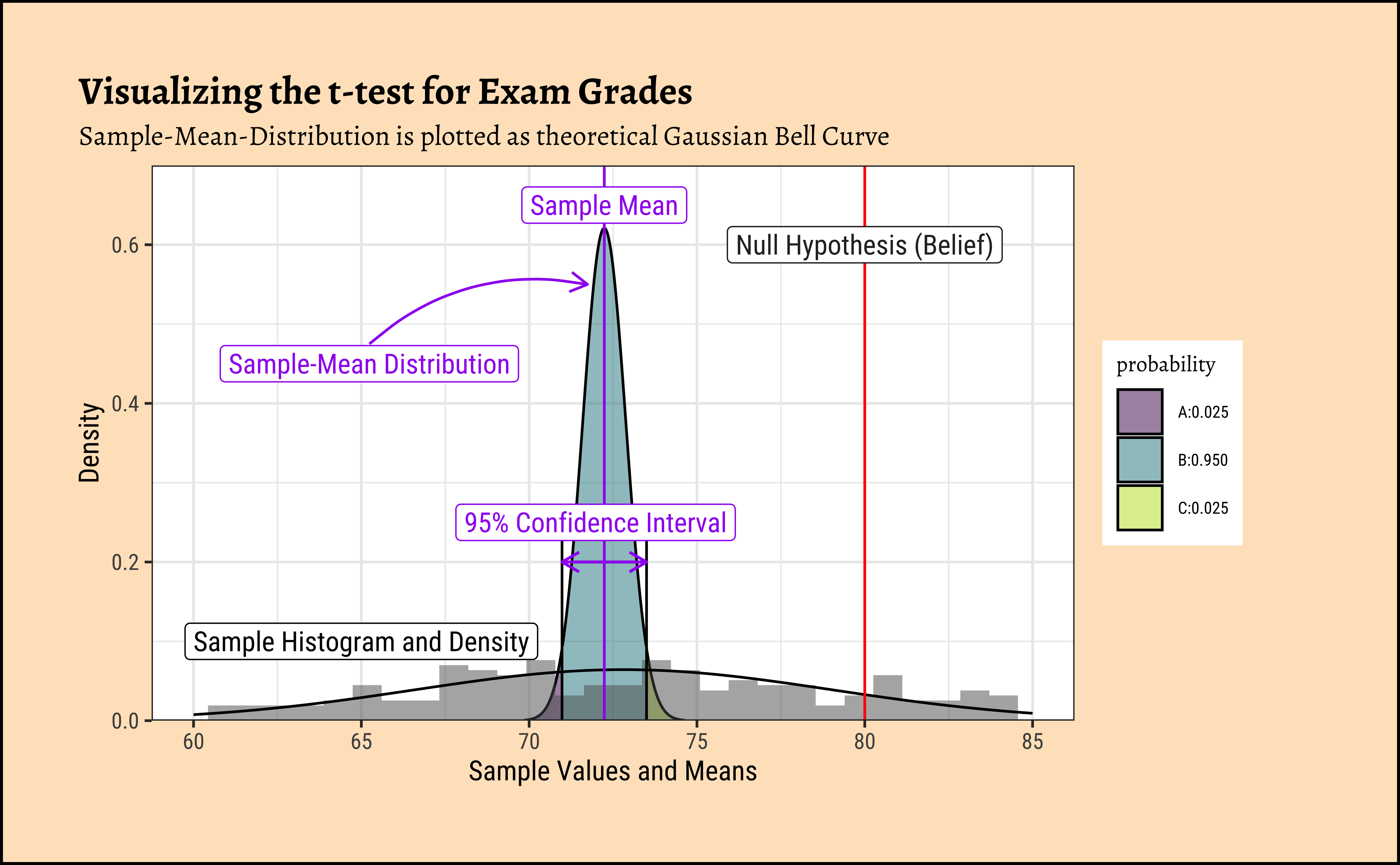
[1] 72.23883

Sample Mean

[1] 80

Null Hypothesis / Belief

[1] 9.807053

Sample Standard Deviation

[1] 0.6424814

Sample Standard Error

[1] -12.07999

Test Statistic

Now let us plot the figure with all these calculations:

Code 
## Let's plot this
## Sample Data
ggplot2::theme_set(new = theme_custom())

mosaic::xqnorm(
  p = c(0.025, 0.975), mean = obs_mean_2, sd = sample_se_2,
  return = c("value"), verbose = T, plot = F
) -> xq2

## Sample-Mean Distribution
xqnorm(
  p = c(0.025, 0.975), mean = obs_mean_2, sd = sample_se_2,
  digits = 3, plot = TRUE,
  return = c("plot"), verbose = F, alpha = 0.5, colour = "black",
  system = "gg"
) %>%
  gf_dhistogram(~course_grade, data = exam_grades, inherit = F) %>%
  gf_fitdistr(~course_grade, data = exam_grades, inherit = F) %>%
  gf_vline(xintercept = obs_mean_2, colour = "purple") %>%
  gf_annotate(
    geom = "label", x = 65, y = 0.1,
    label = "Sample Histogram and Density",
    colour = "black"
  ) %>%
  ## Null
  gf_vline(xintercept = ~mean_belief_pop_2, colour = "red") %>%
  gf_annotate(
    geom = "label", x = mean_belief_pop_2, y = 0.6,
    label = "Null Hypothesis (Belief)"
  ) %>%
  ## Sample Mean and Distribution
  gf_annotate(
    geom = "label", x = obs_mean_2, y = 0.65,
    label = "Sample Mean", colour = "purple"
  ) %>%
  gf_annotate(
    geom = "label", x = obs_mean_2 - 7, y = 0.45,
    label = "Sample-Mean Distribution", colour = "purple"
  ) %>%
  gf_annotate("curve",
    x = obs_mean_2 - 7, y = 0.475,
    xend = obs_mean_2 - 0.5, yend = 0.55,
    curvature = -0.25, color = "purple",
    arrow = arrow(length = unit(0.25, "cm"))
  ) %>%
  ## Z-limits for p = 0.95
  gf_annotate("segment",
    x = obs_mean_2 - 1.96 * sample_se_2, y = 0.0,
    xend = obs_mean_2 - 1.96 * sample_se_2, yend = 0.25
  ) %>%
  gf_annotate("segment",
    x = obs_mean_2 + 1.96 * sample_se_2, y = 0.0,
    xend = obs_mean_2 + 1.96 * sample_se_2, yend = 0.25
  ) %>%
  ## Confidence Intervals
  gf_annotate("segment",
    x = obs_mean_2 - 1.96 * sample_se_2, y = 0.2,
    xend = obs_mean_2 + 1.96 * sample_se_2, yend = 0.2,
    color = "purple", linewidth = 0.5,
    arrow = arrow(length = unit(0.25, "cm"), ends = "both")
  ) %>%
  gf_annotate(
    geom = "label", x = obs_mean_2 - 1.96 * sample_se_2 + 1, y = 0.25,
    label = "95% Confidence Interval",
    colour = "purple"
  ) %>%
  gf_annotate("curve", # CI
    x = xq[2] + 0.05, y = 0.7,
    xend = xq[2] - 0.4, yend = 0.37,
    curvature = 0.25, color = "purple",
    arrow = arrow(length = unit(0.25, "cm"))
  ) %>%
  gf_labs(
    title = "Visualizing the t-test for Exam Grades",
    subtitle = "Sample-Mean-Distribution is plotted as theoretical Gaussian Bell Curve",
    x = "Sample Values and Means", y = "Density"
  ) %>%
  gf_refine(
    scale_y_continuous(limits = c(0, 0.7), expand = expansion(add = c(0, 0))),
    scale_x_continuous(limits = c(60, 85))
  )
Visualizing the t-test for Exam Grades
Figure 8: Sample Distribution, Sample Mean Distribution, and Confidence Intervals

Please see the Section 14 for an Explanation of of this model generated using AI + R.

Workflow for Inference for a Single Mean

A series of tests deal with one mean value of a sample. The idea is to evaluate whether that mean is representative of the mean of the underlying population. Depending upon the nature of the (single) variable, the test that can be used are as follows:

flowchart TD
    A[Inference for Single Mean] -->|Check Assumptions| B[Normality: Shapiro-Wilk Test shapiro.test\n or\n Anderson-Darling Test]
    B --> C{OK?}
    C -->|Yes\n Parametric| D[t.test]
    C -->|No\n Non-Parametric| E[wilcox.test]
    E <--> G[t.test\n with\n Signed-Ranks of Data]
    C -->|No\n Non-Parametric| P[Bootstrap]
    C -->|No\n Non-Parametric| Q[Permutation]

Wait, But Why?

  • We can only sample from a population, and calculate sample statistics
  • But we still want to know about population parameters
  • All our tests and measures of uncertainty with samples are aimed at obtaining a confident measure of a population parameter.
  • Means are the first on the list!

Conclusion

  • If samples are normally distributed, we use a t.test.
  • Else we try non-parametric tests such as the Wilcoxon test.
  • Since we now have compute power at our fingertips, we can leave off considerations of normality and simply proceed with either a permutation or a boostrap test.

References

  1. OpenIntro Modern Statistics, Chapter #17
  2. Bootstrap based Inference using the infer package: https://infer.netlify.app/articles/t_test
  3. Michael Clark & Seth Berry. Models Demystified: A Practical Guide from t-tests to Deep Learning. https://m-clark.github.io/book-of-models/
  4. University of Warwickshire. SAMPLING: Searching for the Approximation Method use to Perform rational inference by Individuals and Groups. https://sampling.warwick.ac.uk/#Overview

Additional Readings

  1. https://mine-cetinkaya-rundel.github.io/quarto-tip-a-day/posts/21-diagrams/
R Package Citations
Package Version Citation
ellmer 0.3.2 Wickham et al. (2025)
infer 1.0.9 Couch et al. (2021)
openintro 2.5.0 Çetinkaya-Rundel et al. (2024)
resampledata 0.3.2 Chihara and Hesterberg (2018)
statlingua 0.1.0 Greenwell (2025)
TeachHist 0.2.1 Lange (2023)
TeachingDemos 2.13 Snow (2024)
Çetinkaya-Rundel, Mine, David Diez, Andrew Bray, Albert Y. Kim, Ben Baumer, Chester Ismay, Nick Paterno, and Christopher Barr. 2024. openintro: Datasets and Supplemental Functions from “OpenIntro” Textbooks and Labs. https://doi.org/10.32614/CRAN.package.openintro.
Chihara, Laura M., and Tim C. Hesterberg. 2018. Mathematical Statistics with Resampling and r. John Wiley & Sons Hoboken NJ. https://github.com/lchihara/MathStatsResamplingR?tab=readme-ov-file.
Couch, Simon P., Andrew P. Bray, Chester Ismay, Evgeni Chasnovski, Benjamin S. Baumer, and Mine Çetinkaya-Rundel. 2021. “infer: An R Package for Tidyverse-Friendly Statistical Inference.” Journal of Open Source Software 6 (65): 3661. https://doi.org/10.21105/joss.03661.
Greenwell, Brandon M. 2025. statlingua: Explain Statistical Output with Large Language Models. https://doi.org/10.32614/CRAN.package.statlingua.
Lange, Carsten. 2023. TeachHist: A Collection of Amended Histograms Designed for Teaching Statistics. https://doi.org/10.32614/CRAN.package.TeachHist.
Snow, Greg. 2024. TeachingDemos: Demonstrations for Teaching and Learning. https://doi.org/10.32614/CRAN.package.TeachingDemos.
Wickham, Hadley, Joe Cheng, Aaron Jacobs, Garrick Aden-Buie, and Barret Schloerke. 2025. ellmer: Chat with Large Language Models. https://doi.org/10.32614/CRAN.package.ellmer.

An AI Generated Explanation of the Statistical Models

We have used the statlingua package to generate an AI explanation of the statistical model t4 we have used in this module. statlingua interfaces to the ellmer package, which in turn interfaces to the ollama API for AI explanations. The AI model used is llama3.1, and the explanation is tailored for a novice audience with moderate verbosity.

AI Generated Explanation

The command was run in the Console and the results pasted into this Quarto document. I have not edited this at all. Do look for complex verbiage and outright hallucinatory responses!!

Code 
library(ellmer)
library(statlingua)
library(chores)
client <- ellmer::chat_ollama(model = "llama3.1", echo = FALSE)
###

exam_context <- "
The model uses a data set on child exam grades from the openintro package in R.
The hypothesis is that the average course grade is 80%. The model includes a t-test and a Wilcoxon signed-rank test to assess whether the mean of the course grades significantly differs from this value.
The variables are:
- `course_grade`: The final grade in the course, which is a numeric variable.
- `semester`: The semester in which the course was taken, which is a factor variable.
- `sex`: Sex of the student ( Man / Woman )
- ` exam1`, `exam2`, `exam3`: Scores on three exams, which are numeric variables.
The model also includes a permutation test and a bootstrap test to further assess the hypothesis."

explanation4 <- statlingua::explain(t4,
  client = client,
  context = exam_context,
  audience = "novice", verbosity = "moderate"
) # moderate / detailed

One-Sample t-test Output Interpretation

This is a One-sample t-test output summary from R, comparing the mean course grade (course_grade) against 80%. Key elements are outlined below:

Estimate, Statistic, p-value, and N/A Parameter

  • estimate (72.2):
    • Indicates the estimated sample mean of course_grade, in this case approximately 72.2.
    • This suggests that on average, across all examined children, their final grades are below 80%.
  • statistic (-12.1):
    • The large negative value indicates how many standard deviations away from the hypothesized mean (\(80\)) our observed estimate is; this can help us grasp just how ‘unexpected’ our outcome really is.
    • This large difference would usually correspond to a very small p-value under \(H_0\), which supports rejecting it.
  • p-value (2.19e-26):
    • Extremely low p-values (usually below 0.05 or even .001) indicate that the observed effect or deviation from the expected value is statistically significant.
    • In this context, the hypothesis of 80% being the true mean can be strongly rejected since achieving such a grade as often as observed purely by chance for our sample size is incredibly unlikely.
  • parameter (232):
    • The parameter usually refers to the degrees of freedom used in the calculation of test statistics.
    • However, since we’re looking at one sample t-test results here it likely indicates that there are 231 data points or more as ‘available’. A large such number is expected given that often this statistic simply becomes irrelevant to further inferences about such hypotheses (especially those based on a normal distribution assumption), because for larger n approaching population size all t-statistics should effectively be treated identically and become useless for exact confidence intervals etc..

Confidence Intervals

  • conf.low and conf.high: These provide bounds within which the true mean can be estimated not to lie with 95% probability, given our understanding of the test’s results so far.

Additional Details

  • method: Often ‘One Sample’, as seen in this example. One-sample tests are used when comparing an individual sample or a group of samples against a known population parameter.
  • alternative: This denotes the directionality assumption during hypothesis testing; by default it is set to two-sided for most statistical tests, which means we want to determine whether our result (if any) contradicts H0 in either direction (above or below, greater or smaller). There are one-tailed tests too though which look at differences only above (> or <), not both sides.

Remember, given the small p-value (.0022e+26 being effectively zero), you can reject H0 very safely and conclude that observed exam grade averages definitely differ significantly from what we’d expect if things were as described in our model according to a normal probability distribution. The large t-statistic (-12, indicating substantial deviation) confirms this.