library(tidyverse)
library(mosaic) # Our go-to package
library(ggformula)
library(infer) # An alternative package for inference using tidy data
library(broom) # Clean test results in tibble form
library(skimr) # data inspection
library(tinytable) # Pretty Tables
library(kableExtra) # Pretty Tables
library(ggprism) # Prism-like ggplot themes
##
library(visStatistics) # All-in-one Stats test package
##
library(resampledata3) # Datasets from Chihara and Hesterberg's book
library(openintro) # datasetsInference for Two Independent Means
How diff-different(sic) are you?
2022-11-22
To be nobody but myself – in a world which is doing its best, night and day, to make you everybody else – means to fight the hardest battle which any human being can fight, and never stop fighting.
— E.E. Cummings, poet (14 Oct 1894-1962)
Plot Fonts and Theme
Code
library(systemfonts)
library(showtext)
## Clean the slate
systemfonts::clear_local_fonts()
systemfonts::clear_registry()
##
showtext_opts(dpi = 96) # set DPI for showtext
sysfonts::font_add(
family = "Alegreya",
regular = "../../../../../../fonts/Alegreya-Regular.ttf",
bold = "../../../../../../fonts/Alegreya-Bold.ttf",
italic = "../../../../../../fonts/Alegreya-Italic.ttf",
bolditalic = "../../../../../../fonts/Alegreya-BoldItalic.ttf"
)
sysfonts::font_add(
family = "Roboto Condensed",
regular = "../../../../../../fonts/RobotoCondensed-Regular.ttf",
bold = "../../../../../../fonts/RobotoCondensed-Bold.ttf",
italic = "../../../../../../fonts/RobotoCondensed-Italic.ttf",
bolditalic = "../../../../../../fonts/RobotoCondensed-BoldItalic.ttf"
)
showtext_auto(enable = TRUE) # enable showtext
##
theme_custom <- function() {
theme_bw(base_size = 10) +
# theme(panel.widths = unit(11, "cm"),
# panel.heights = unit(6.79, "cm")) + # Golden Ratio
theme(
plot.margin = margin_auto(t = 1, r = 2, b = 1, l = 1, unit = "cm"),
plot.background = element_rect(
fill = "bisque",
colour = "black",
linewidth = 1
)
) +
theme_sub_axis(
title = element_text(
family = "Roboto Condensed",
size = 10
),
text = element_text(
family = "Roboto Condensed",
size = 8
)
) +
theme_sub_legend(
text = element_text(
family = "Roboto Condensed",
size = 6
),
title = element_text(
family = "Alegreya",
size = 8
)
) +
theme_sub_plot(
title = element_text(
family = "Alegreya",
size = 14, face = "bold"
),
title.position = "plot",
subtitle = element_text(
family = "Alegreya",
size = 10
),
caption = element_text(
family = "Alegreya",
size = 6
),
caption.position = "plot"
)
}
## Use available fonts in ggplot text geoms too!
ggplot2::update_geom_defaults(geom = "text", new = list(
family = "Roboto Condensed",
face = "plain",
size = 3.5,
color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "label", new = list(
family = "Roboto Condensed",
face = "plain",
size = 3.5,
color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "marquee", new = list(
family = "Roboto Condensed",
face = "plain",
size = 3.5,
color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "text_repel", new = list(
family = "Roboto Condensed",
face = "plain",
size = 3.5,
color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "label_repel", new = list(
family = "Roboto Condensed",
face = "plain",
size = 3.5,
color = "#2b2b2b"
))
## Set the theme
ggplot2::theme_set(new = theme_custom())
## tinytable options
options("tinytable_tt_digits" = 2)
options("tinytable_format_num_fmt" = "significant_cell")
options(tinytable_html_mathjax = TRUE)
## Set defaults for flextable
flextable::set_flextable_defaults(font.family = "Roboto Condensed")
Sometimes, we need to compare if two distinct populations have the same mean. For instance we may wish to compare salaries between two different professions, or test scores between two different teaching methods. In this case, we take a sample ( not necessarily of equal length ) from each population, and compare the means of the two samples.
Here is a diagram showing the workflow of this test based on the kind of data samples we encounter.
flowchart TD
A[Inference for Two Independent Means] -->|Check Assumptions| B[Normality: Shapiro-Wilk Test shapiro.test Variances: Fisher F-test var.test]
B --> C{OK?}
C -->|Yes, both Parametric| D[t.test]
C -->|Yes, but not variance Parametric| W[t.test with Welch Correction]
C -->|No Non-Parametric| E[wilcox.test]
E <--> G[Linear Model with Signed-Ranks]
C -->|No Non-Parametric| P[Bootstrap or Permutation]
Let us look at the MathAnxiety dataset from the package resampledata. Here we have “anxiety” scores for boys and girls, for different components of mathematics.
Rows: 599
Columns: 6
$ Age <dbl> 137.8, 140.7, 137.9, 142.8, 135.6, 135.0, 133.6, 139.3, 131.7, …
$ Gender <fct> Boy, Boy, Girl, Girl, Boy, Girl, Boy, Boy, Girl, Boy, Boy, Boy,…
$ Grade <fct> Secondary, Secondary, Secondary, Secondary, Secondary, Secondar…
$ AMAS <int> 9, 18, 23, 19, 23, 27, 22, 17, 28, 20, 16, 20, 21, 36, 16, 27, …
$ RCMAS <int> 20, 8, 26, 18, 20, 33, 23, 11, 32, 30, 10, 4, 23, 26, 24, 21, 3…
$ Arith <int> 6, 6, 5, 7, 1, 1, 4, 7, 2, 6, 2, 5, 2, 6, 2, 7, 2, 4, 7, 3, 8, …| skim_type | skim_variable | n_missing | complete_rate | factor.ordered | factor.n_unique | factor.top_counts | numeric.mean | numeric.sd | numeric.p0 | numeric.p25 | numeric.p50 | numeric.p75 | numeric.p100 | numeric.hist |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| factor | Gender | 0 | 1 | FALSE | 2 | Boy: 323, Gir: 276 | NA | NA | NA | NA | NA | NA | NA | NA |
| factor | Grade | 0 | 1 | FALSE | 2 | Pri: 401, Sec: 198 | NA | NA | NA | NA | NA | NA | NA | NA |
| numeric | Age | 0 | 1 | NA | NA | NA | 125 | 22 | 3.7 | 106 | 121 | 142 | 188 | ▁▁▇▇▃ |
| numeric | AMAS | 0 | 1 | NA | NA | NA | 22 | 6.6 | 4 | 18 | 22 | 26 | 45 | ▂▆▇▃▁ |
| numeric | RCMAS | 0 | 1 | NA | NA | NA | 19 | 7.6 | 1 | 14 | 19 | 25 | 41 | ▂▇▇▅▁ |
| numeric | Arith | 0 | 1 | NA | NA | NA | 5.3 | 2.1 | 0 | 4 | 6 | 7 | 8 | ▂▃▃▇▇ |
The MathAnxiety dataset contains data on students’ anxiety levels, with ~600 data observations.
Quantitative Data
Age: Age of the student (in years)AMAS: Anxiety score from the Abbreviated Math Anxiety Scale (AMAS)RCMAS: Anxiety score from the Revised Children’s Manifest Anxiety Scale (RCMAS)Arith: Score on Arithmetic Test
Qualitative Data
Gender: Boy / GirlGrade: Grade level of the student (e.g., 5th, 6th, etc.)
- The target variable-s for an experiment that resulted in this data might be either of the two Anxiety-related scores.
Research Question
- Is there a difference between
BoyandGirl“anxiety” levels forAMAS(test) in the population from which the MathAnxiety dataset is a sample? - Ditto for the
RCMASscores - Apropos: We may also be interested in the correlation between the anxiety-related variables and the
Arithscore obtained, and if it differs betweenBoys andGirls.
First, histograms, densities and counts of the variable we are interested in, after converting data into long format:
Code
Code
# Set graph theme
theme_set(new = theme_custom())
# https://www.statology.org/r-geom_path-each-group-consists-of-only-one-observation/
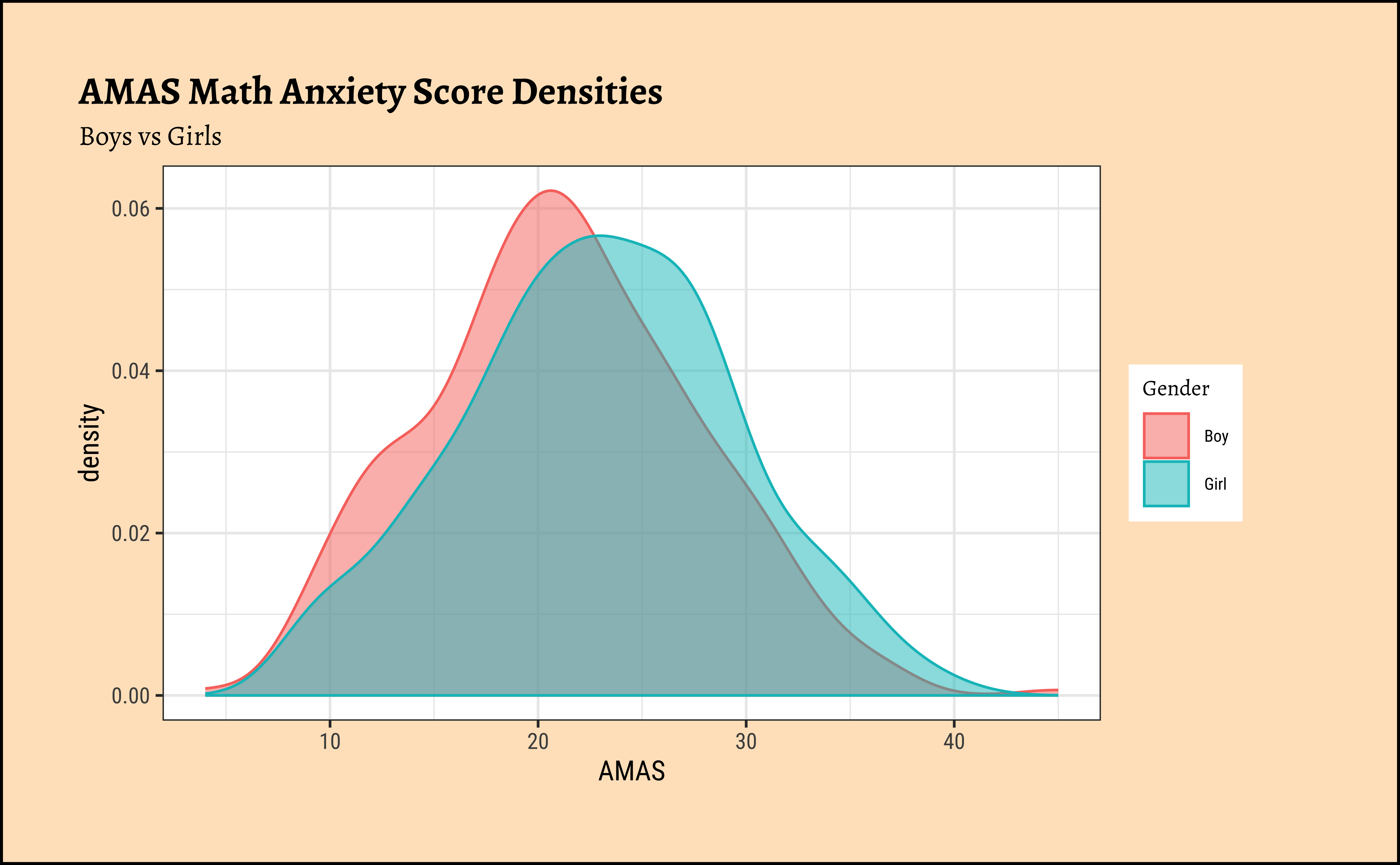
MathAnxiety %>%
gf_density(
~AMAS,
fill = ~Gender, colour = ~Gender,
alpha = 0.5,
title = "AMAS Math Anxiety Score Densities",
subtitle = "Boys vs Girls"
)
##
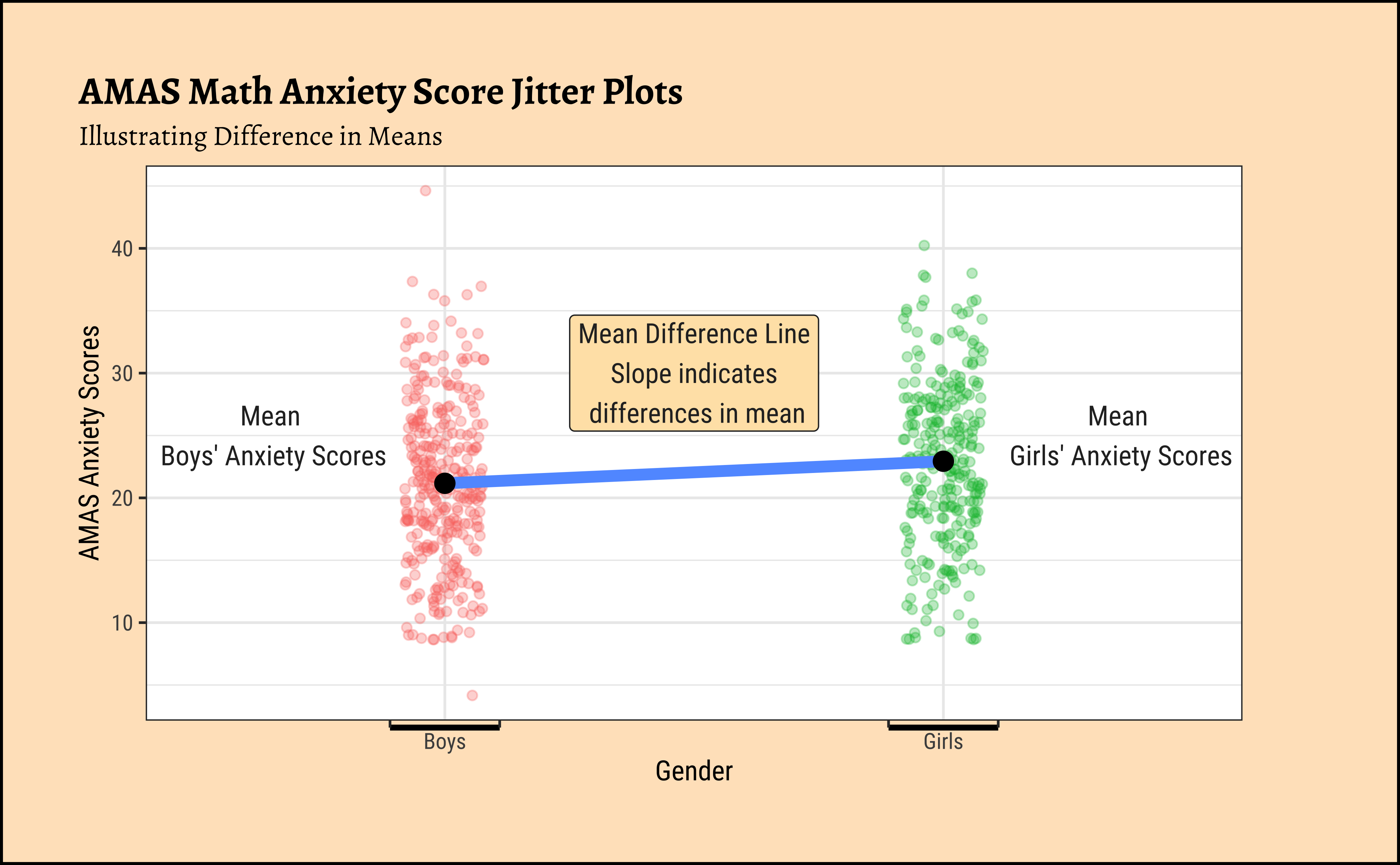
MathAnxiety %>%
pivot_longer(
cols = -c(Gender, Age, Grade),
names_to = "type",
values_to = "value"
) %>%
dplyr::filter(type == "AMAS") %>%
gf_jitter(
value ~ Gender,
group = ~type, color = ~Gender,
width = 0.08, alpha = 0.3,
ylab = "AMAS Anxiety Scores",
title = "AMAS Math Anxiety Score Jitter Plots",
subtitle = "Illustrating Difference in Means"
) %>%
gf_summary(
group = ~1, # Damn!!! Look at the reference link above
fun = "mean", geom = "line",
colour = ~"MeanDifferenceLine",
lty = 1, linewidth = 2
) %>%
gf_summary(geom = "point", size = 3, colour = "black") %>%
gf_refine(scale_x_discrete(
breaks = c("Boy", "Girl"),
labels = c("Boys", "Girls"),
guide = guide_prism_bracket(width = 0.1, outside = FALSE)
)) %>%
gf_annotate(x = 0.65, y = 25, geom = "text", label = "Mean\n Boys' Anxiety Scores", family = "Roboto Condensed") %>%
gf_annotate(x = 2.35, y = 25, geom = "text", label = "Mean\n Girls' Anxiety Scores", family = "Roboto Condensed") %>%
gf_annotate(x = 1.5, y = 30, geom = "label", label = "Mean Difference Line\nSlope indicates\n differences in mean", fill = "moccasin", family = "Roboto Condensed") %>%
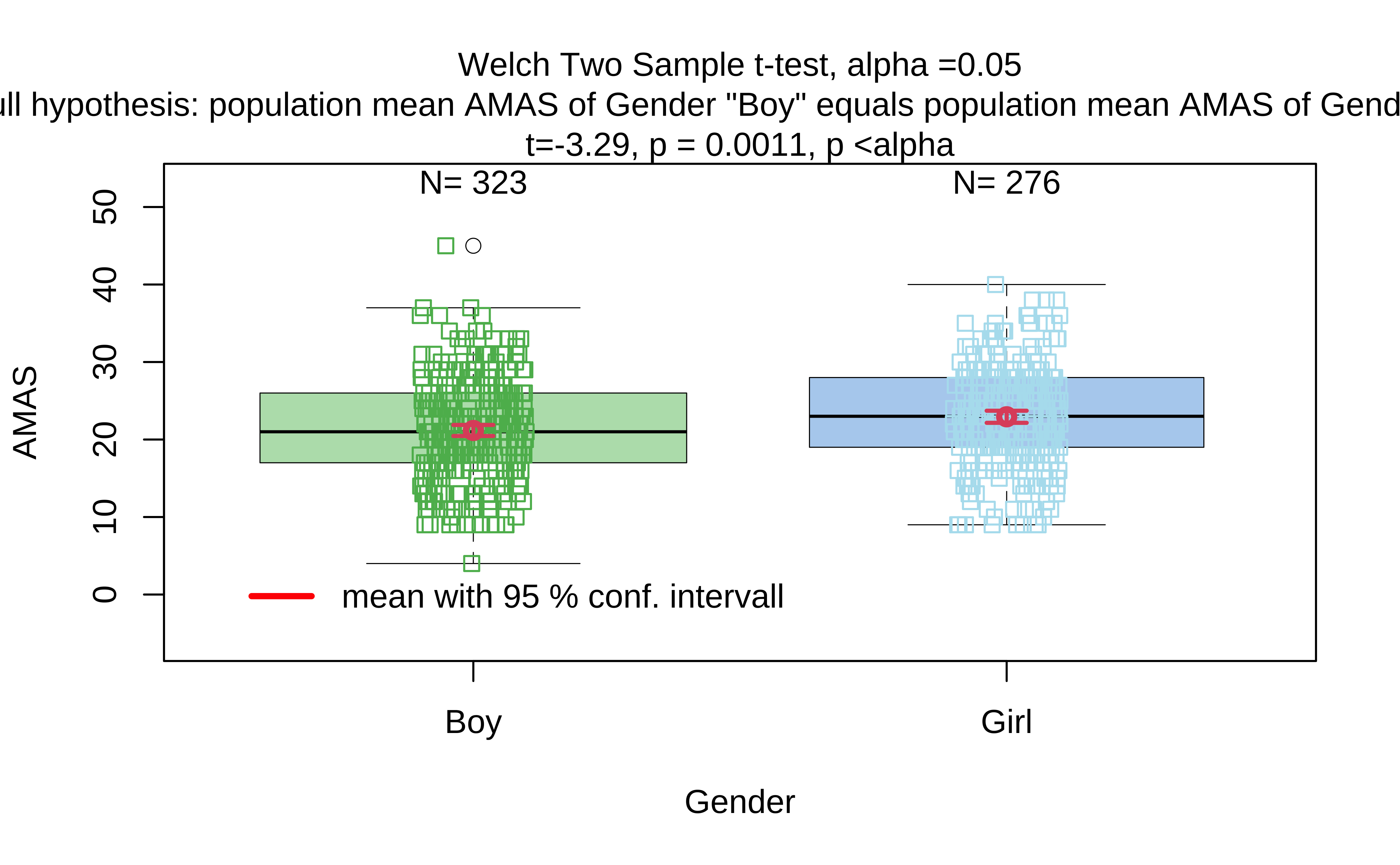
gf_theme(theme(legend.position = "none", axis.line.x = element_line(linewidth = 1)))The distributions for anxiety scores for boys and girls overlap considerably and are very similar, though the jitter plot for boys shows significant outliers. Are they close to being normal distributions too? We should check.
A.
Statistical tests for means usually require a couple of checks1 2:
- Are the data normally distributed?
- Are the data variances similar?
Let us complete a check for normality: the shapiro.wilk test checks whether a Quant variable is from a normal distribution; the NULL hypothesis is that the data are from a normal distribution. We will also look at Q-Q plots for both variables:
Code
# Set graph theme
theme_set(new = theme_custom())
#
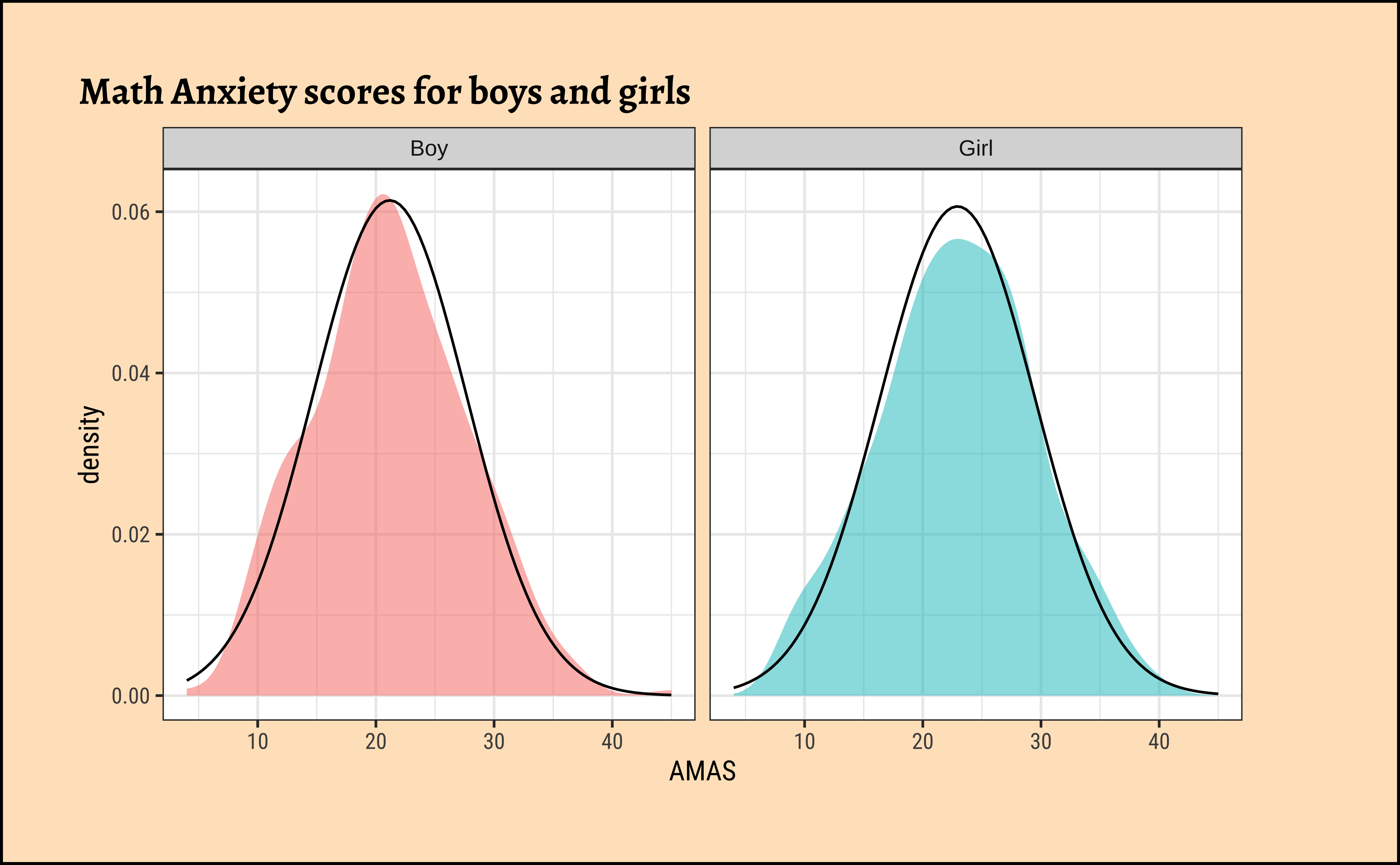
MathAnxiety %>%
gf_density(~AMAS,
fill = ~Gender,
alpha = 0.5,
title = "Math Anxiety scores for boys and girls"
) %>%
gf_facet_grid(~Gender) %>%
gf_fitdistr(dist = "dnorm") %>%
gf_theme(theme(legend.position = "none")) # No Need!!
##
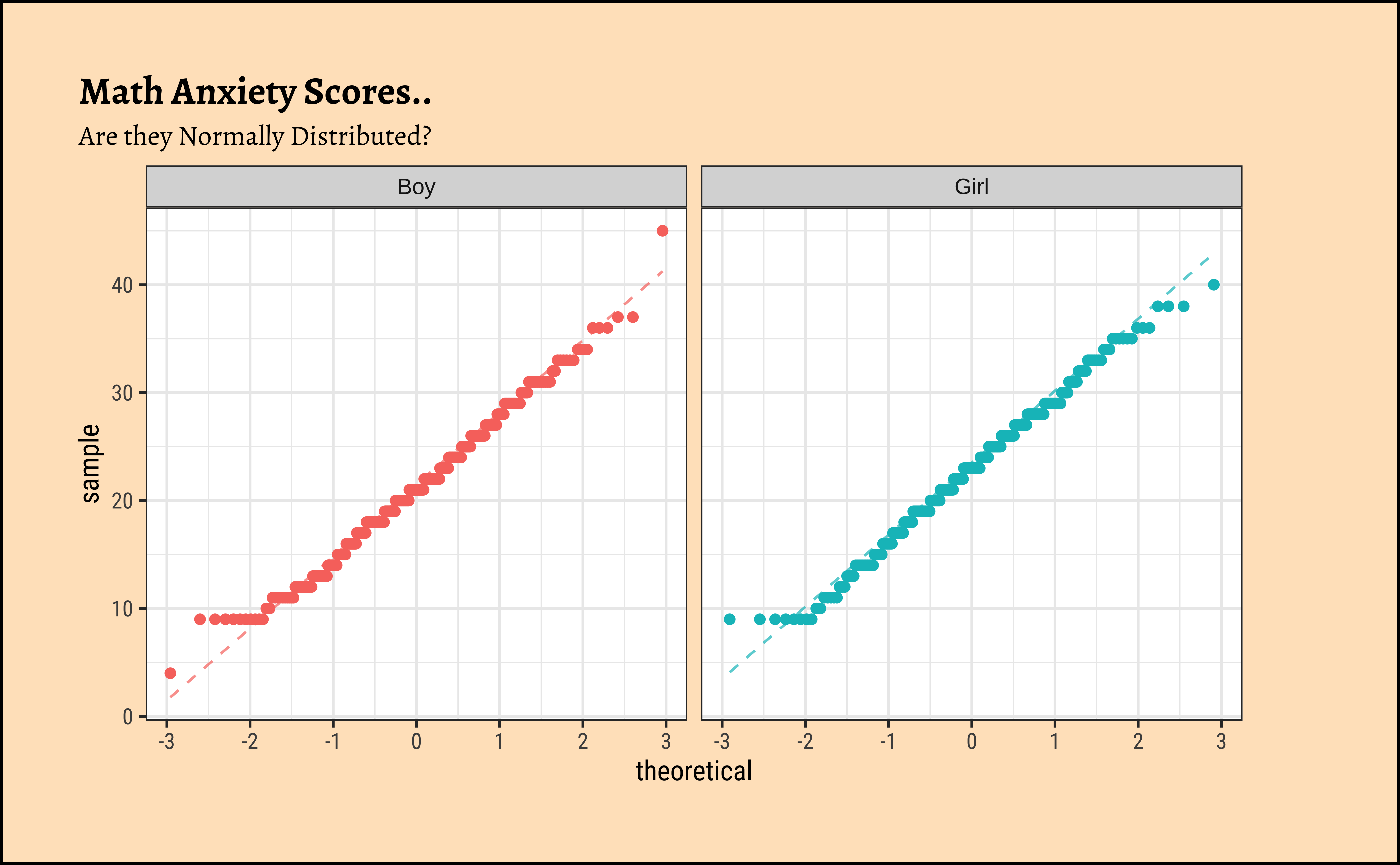
MathAnxiety %>%
gf_qqline(~AMAS,
color = ~Gender,
title = "Math Anxiety Scores..",
subtitle = "Are they Normally Distributed?"
) %>%
gf_qq() %>%
gf_facet_wrap(~Gender) %>% # independent y-axis
gf_theme(theme(legend.position = "none")) # No Need!!Let us split the dataset into subsets, to execute the normality check test (Shapiro-Wilk test):
Shapiro-Wilk normality test
data: boys_AMAS$AMAS
W = 0.99043, p-value = 0.03343
Shapiro-Wilk normality test
data: girls_AMAS$AMAS
W = 0.99074, p-value = 0.07835The distributions for anxiety scores for boys and girls are almost normal, visually speaking. With the Shapiro-Wilk test we find that the scores for girls are normally distributed, but the boys scores are not so. Tch, tch. These boys.
Note
The p.value obtained in the shapiro.wilk test suggests the chances of the data being so, given the Assumption that they are normally distributed.
We see that MathAnxiety contains discrete-level scores for anxiety for the two variables (for Boys and Girls) anxiety scores. The boys score has a significant outlier, which we saw earlier and perhaps that makes that variable lose out, perhaps narrowly.
B.
Let us check if the two variables have similar variances: the var.test does this for us, with a NULL hypothesis that the variances are not significantly different:
[1] 1.254823The variances are quite similar as seen by the \(p.value = 0.82\). We also saw it visually when we plotted the overlapped distributions earlier.
Conditions:
- The two variables are not both normally distributed.
- The two variances are significantly similar.
Based on the graphs, how would we formulate our Hypothesis? We wish to infer whether there is any difference in the mean anxiety score between Girls and Boys, in the population from which the dataset MathAnxiety has been drawn. So accordingly:
\[ H_0: \mu_{Boys} - \mu_{Girls} = 0\\ \]
\[ H_a: \mu_{Boys} - \mu_{Girls} \ne 0\\ \]
What would be the test statistic we would use? The difference in means. Is the observed difference in the means between the two groups of scores non-zero? We use the diffmean function:
Girls’ AMAS anxiety scores are, on average, \(1.76\) points higher than those for Boys in the dataset/sample.
On Observed Difference Estimates
Different tests here will show the difference as positive or negative, but with the same value! This depends upon the way the factor variable Gender is used, i.e. Boy-Girl or Girl-Boy…
- Parametric t.test
- Mann-Whitney Test
- Linear Model Interpretation
- Permutation Test
- Visual and by Hand t.test
Since the data are not both normally distributed, though the variances similar, we typically cannot use a parametric t.test. However, we can still examine the results:
The p.value is \(0.001\) ! And the Confidence Interval does not straddle \(0\). So the t.test gives us good reason to reject the Null Hypothesis that the means are similar and that there is a significant difference between Boys and Girls when it comes to AMAS anxiety. But can we really believe this, given the non-normality of data?
Since the data variables do not satisfy the assumption of being normally distributed, and though the variances are similar, we use the classical wilcox.test (Type help(wilcox.test) in your Console.) which implements what we need here: the Mann-Whitney U test:1
The Mann-Whitney test as a test of mean ranks. It first ranks all your values from high to low, computes the mean rank in each group, and then computes the probability that random shuffling of those values between two groups would end up with the mean ranks as far apart as, or further apart, than you observed. No assumptions about distributions are needed so far. (emphasis mine)
\[ mean(rank(AMAS_{Girls})) - mean(rank(AMAS_{Boys})) = diff \]
\[ H_0: \mu_{Boys} - \mu_{Girls} = 0 \]
\[ H_a: \mu_{Boys} - \mu_{Girls} \ne 0 \]
Code
library(ggprism)
library(ggtext)
library(glue)
library(latex2exp)
# https://www.statology.org/r-geom_path-each-group-consists-of-only-one-observation/
# Set graph theme
theme_set(new = theme_custom())
#
MathAnxiety %>%
gf_jitter(rank(AMAS) ~ Gender,
color = ~Gender,
show.legend = FALSE,
width = 0.05, alpha = 0.25,
ylab = "Ranks of AMAS anxiety scores",
title = "Ranked Math Anxiety Scores for Boys and Girls"
) %>%
gf_summary(
group = ~1, # See the reference link above. Damn!!!
fun = "mean", geom = "line", colour = "lightblue",
lty = 1, linewidth = 2
) %>%
gf_summary(fun = "mean", colour = "firebrick", size = 4, geom = "point") %>%
gf_refine(scale_x_discrete(
breaks = c("Boy", "Girl"),
labels = c("Boy", "Girl"),
guide = "prism_bracket"
)) %>%
# gf_annotate("label", label = TeX(r"(\textbf{Slope} $mu_{Rank Boys}-mu_{Rank Girls} \neq 0$ )"), y = 500, x = 1.5,
# color = "black", fill = "moccasin") %>%
gf_annotate("label",
label = "Mean Rank \nBoys Scores",
y = 300, x = 0.75, inherit = FALSE
) %>%
gf_annotate("label",
label = "Mean Rank \nGirls Scores",
y = 320, x = 2.25, inherit = FALSE
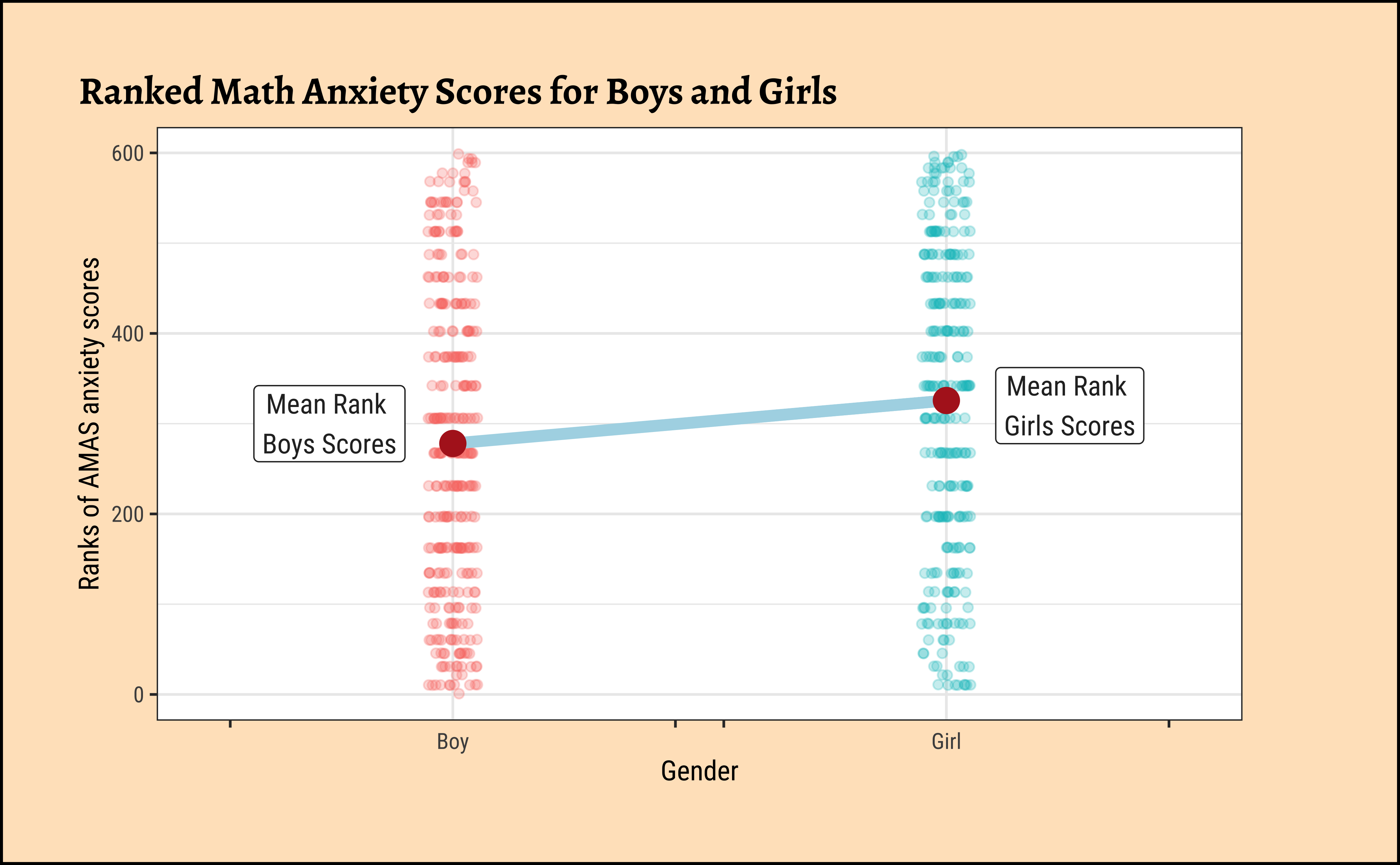
)This is pretty similar to Figure 1 (b) with actual scores. Here we have plotted the ranks of the scores.
The p.value is very similar, \(0.00077\), and again the Confidence Interval does not straddle \(0\), and we are hence able to reject the NULL hypothesis that the means are equal and accept the alternative hypothesis that there is a significant difference in mean anxiety scores between Boys and Girls.
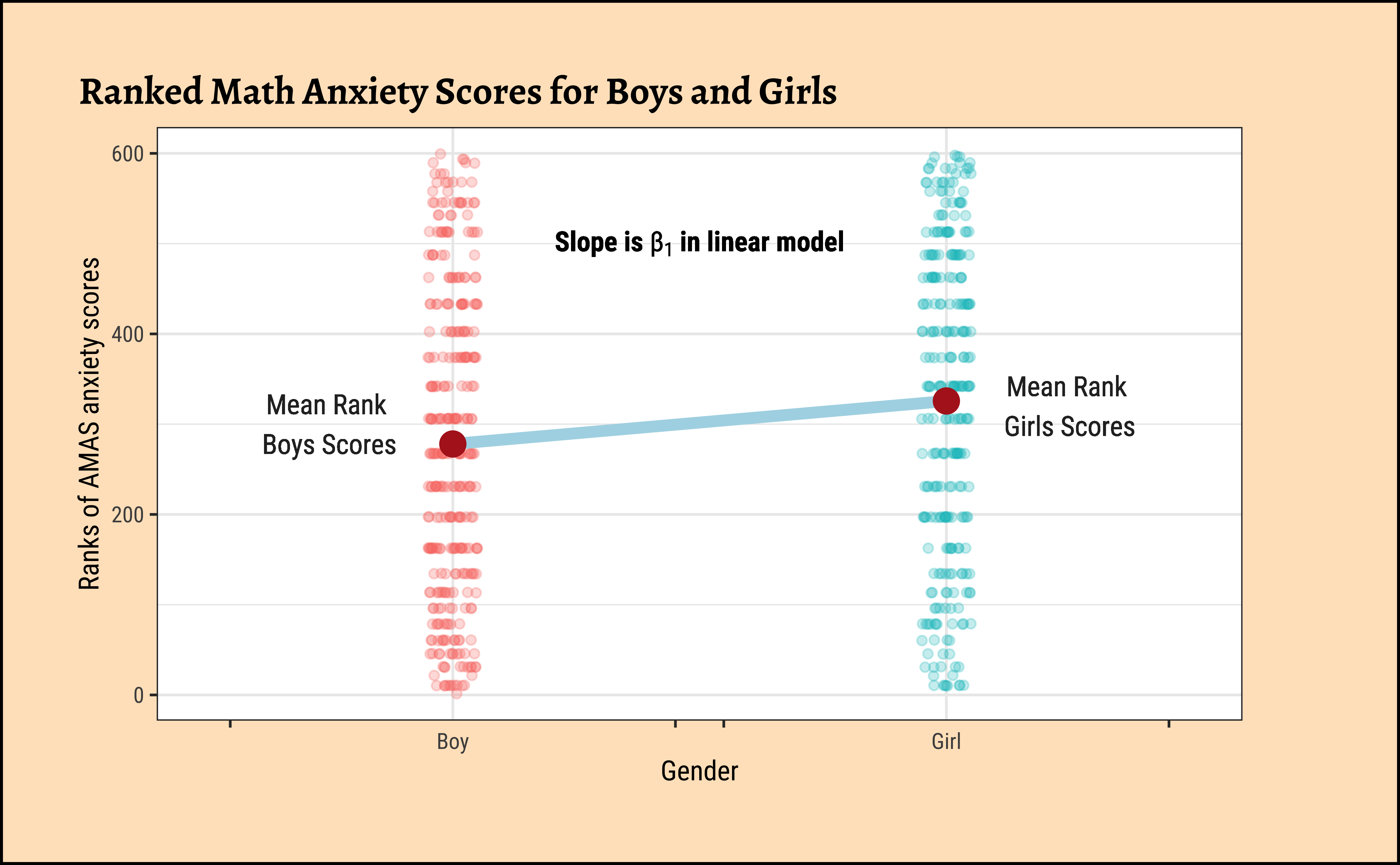
We can apply the linear-model-as-inference interpretation to the ranked data data to implement the non-parametric test as a Linear Model:
\[ lm(rank(AMAS) \sim gender) = \beta_0 + \beta_1 * gender \]
\[ H_0: \beta_1 = 0\\ \]
\[ H_a: \beta_1 \ne 0\\ \]
Code
library(ggprism)
library(ggtext)
library(glue)
library(latex2exp)
# https://www.statology.org/r-geom_path-each-group-consists-of-only-one-observation/
ggplot2::theme_set(new = theme_custom())
MathAnxiety %>%
gf_jitter(rank(AMAS) ~ Gender,
color = ~Gender,
show.legend = FALSE,
width = 0.05, alpha = 0.25,
ylab = "Ranks of AMAS anxiety scores",
title = "Ranked Math Anxiety Scores for Boys and Girls"
) %>%
gf_summary(
group = ~1, # See the reference link above. Damn!!!
fun = "mean", geom = "line", colour = "lightblue",
lty = 1, linewidth = 2
) %>%
gf_summary(fun = "mean", colour = "firebrick", size = 4, geom = "point") %>%
gf_refine(scale_x_discrete(
breaks = c("Boy", "Girl"),
labels = c("Boy", "Girl"),
guide = "prism_bracket"
)) %>%
gf_text(
label = TeX(r"(\textbf{Slope is} $beta_1$ \textbf{in linear model})", output = "character"),
parse = TRUE, 500 ~ 1.5,
color = "black", fill = "moccasin"
) %>%
gf_text(
label = "Mean Rank \nBoys Scores",
300 ~ 0.75, inherit = FALSE
) %>%
gf_text(
label = "Mean Rank \nGirls Scores",
320 ~ 2.25, inherit = FALSE
)Dummy Variables in lm
Note how the Qual variable was used here in Linear Regression! The Gender variable was treated as a binary “dummy” variable2.
Here too we see that the p.value for the slope term (“GenderGirl”) is significant at \(7.4*10^{-4}\).
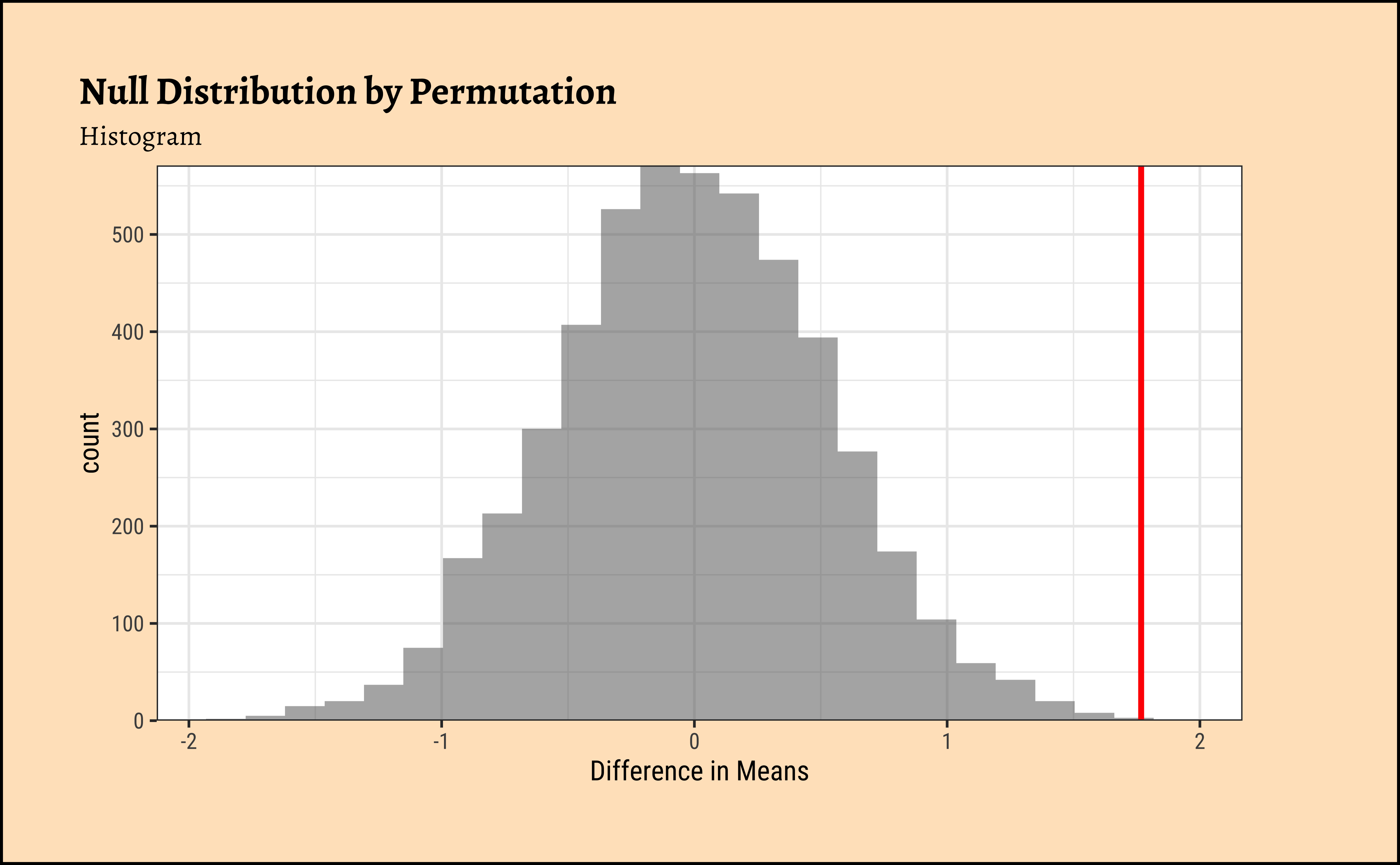
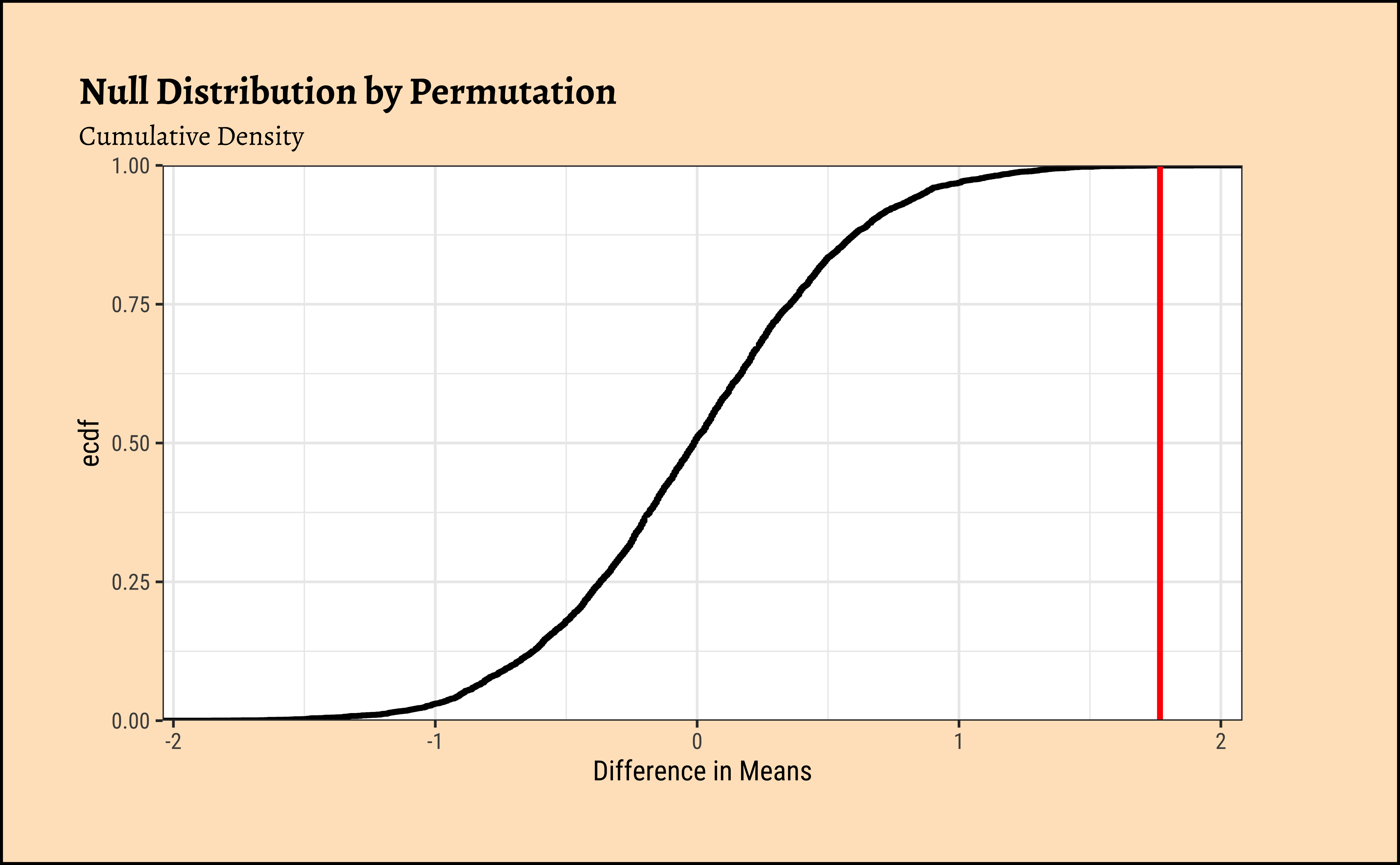
We pretend that Gender has no effect on the AMAS anxiety scores. If this is our position, then the Gender labels are essentially meaningless, and we can pretend that any AMAS score belongs to a Boy or a Girl. This means we can mosaic::shuffle (permute) the Gender labels and see how uncommon our real data is. And we do not have to really worry about whether the data are normally distributed, or if their variances are nearly equal.
Important
The “pretend” position is exactly the NULL Hypothesis!! The “uncommon” part is the p.value under NULL!!
Code
ggplot2::theme_set(new = theme_custom())
gf_histogram(data = null_dist_amas, ~diffmean, bins = 25) %>%
gf_vline(
xintercept = obs_diff_amas,
colour = "red", linewidth = 1,
title = "Null Distribution by Permutation",
subtitle = "Histogram"
) %>%
gf_labs(x = "Difference in Means") %>%
gf_refine(scale_y_continuous(expand = c(0, 0)))
###
gf_ecdf(
data = null_dist_amas, ~diffmean,
linewidth = 1
) %>%
gf_vline(
xintercept = obs_diff_amas,
colour = "red", linewidth = 1,
title = "Null Distribution by Permutation",
subtitle = "Cumulative Density"
) %>%
gf_labs(x = "Difference in Means") %>%
gf_refine(scale_y_continuous(expand = c(0, 0)))Clearly the observed_diff_amas is much beyond anything we can generate with permutations with gender! And hence there is a significant difference in weights across gender!
Here too, as with the Test for a Single Mean, the inner mechanism of the t-test is very similar, but for some important differences:
- Two Means: Calculate the
meanof the two samples \(\bar{x}\) and \(\bar{y}\). - Take the difference between the two sample means \(\bar{x} - \bar{y}\): \[ \text{Difference} = \bar{x} - \bar{y} \]
- Net Variance: Here we need to pool in the variances of both samples and compute the net variance
- Calculate the
standard error(using net-variance) as follows: \[ SE = \sqrt{\frac{s_x^2}{n_x} + \frac{s_y^2}{n_y}} \] where \(s_x\) and \(s_y\) are the standard deviations of the two samples, and \(n_x\) and \(n_y\) are their respective sample sizes. - Scale the difference by the
standard errorto get atest statistic\(t\). \[ t = \frac{\text{Difference}}{SE} \] - If the
test statisticis more than \(\pm 1.96\), we can say that it is beyond the theconfidence intervalof the sample mean difference \(\bar{x} - \bar{y}\) \[ \text{Confidence Interval} = \bar{x} - \bar{y} \pm 1.96 \times SE \] - Therefore if the actual difference and bis far beyond the confidence interval, hmm…we cannot think our belief is correct and we change our opinion that the two means \(\bar{x}\) and \(\bar{y}\) are the same.
Let us translate that mouthful into calculations!
(mean_diff_belief <- 0.0) # Assert our belief
(obs_diff_amas <- diffmean(AMAS ~ Gender, data = MathAnxiety) %>% as.numeric())
(MathAnxiety %>%
dplyr::select(AMAS, Gender) %>%
dplyr::group_by(Gender) %>%
dplyr::summarize(variance = var(AMAS), n = n()) %>%
dplyr::mutate(se_contribution = variance / n) %>%
dplyr::summarise(std_error = sqrt(sum(se_contribution))) %>%
as.numeric() -> std_error_diff)
(conf_int2 <- tibble(ci_low = obs_diff_amas - 1.96 * std_error_diff, ci_high = obs_diff_amas + 1.96 * std_error_diff))
(t <- (obs_diff_amas - mean_diff_belief) / std_error_diff)[1] 0Null Hypothesis / Belief
[1] 1.7676Observed Difference in Means
[1] 0.5369636Standard Error
Confidence Intervals
[1] 3.291843Test Statistic
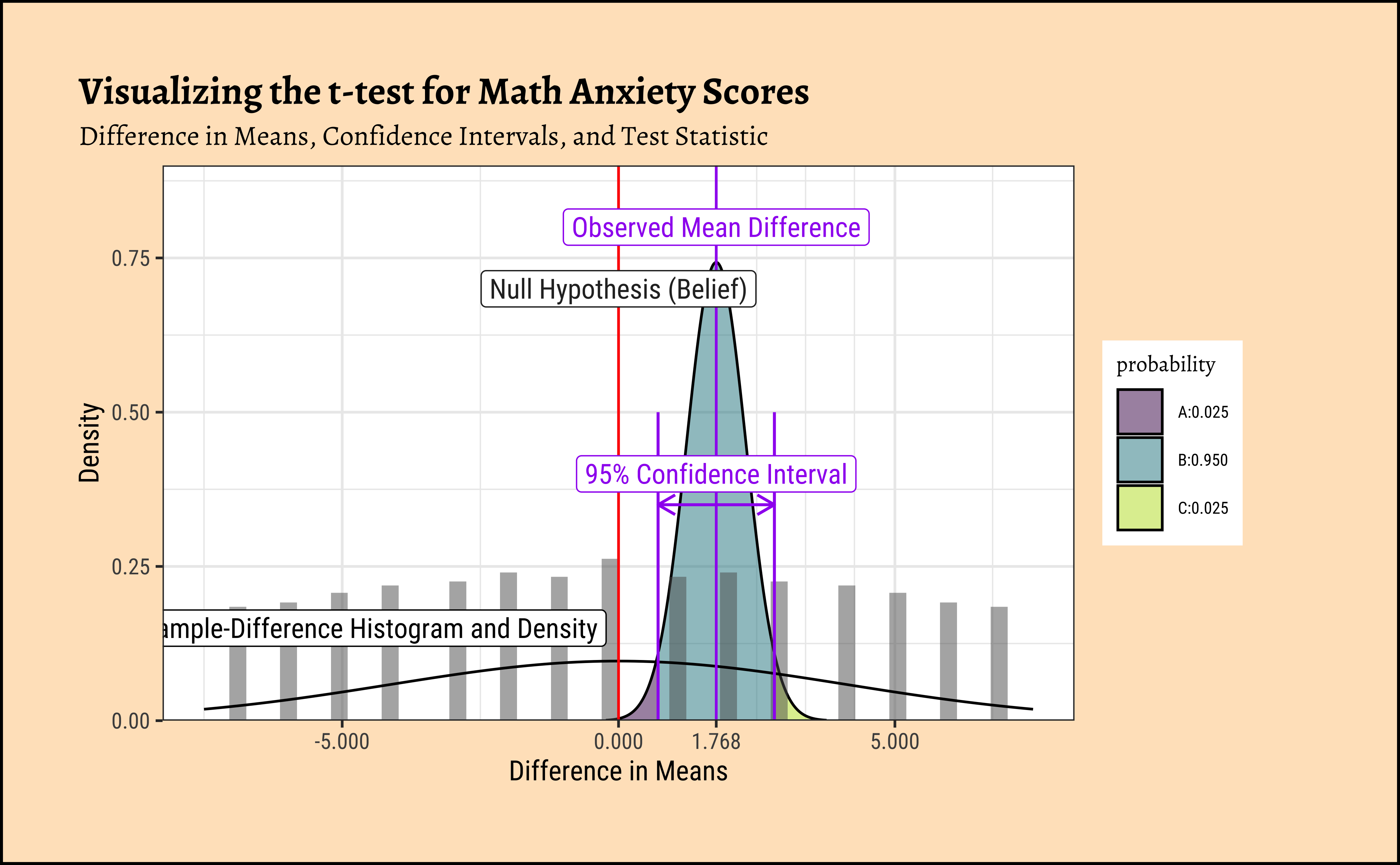
How can we visualize this? We are going to have to construct a difference dataset containing all possible differences between the two groups, and then plot the distribution of those differences. We can then visualize the observed difference in means, the confidence intervals, and the test statistic. Let’see if that works!
Code
ggplot2::theme_set(new = theme_custom())
boys_scores <- boys_AMAS %>% rename("boys" = AMAS)
girls_scores <- boys_AMAS %>% rename("girls" = AMAS)
all_diff <- expand_grid(boys_scores, girls_scores) %>% mutate(diff = boys - girls)
##
mosaic::xqnorm(
p = c(0.025, 0.975), mean = obs_diff_amas, sd = std_error_diff,
return = c("value"), verbose = T, plot = F
) -> xq1
xqnorm(
p = c(0.025, 0.975), mean = obs_diff_amas, sd = std_error_diff,
digits = 3, plot = TRUE,
return = c("plot"), verbose = F, alpha = 0.5, colour = "black",
system = "gg"
) %>%
gf_dhistogram(~diff,
data = all_diff, bins = 50,
xlab = "Difference in Means",
ylab = "Density", inherit = F
) %>% ## Very important!
gf_fitdistr(~diff, data = all_diff, inherit = F) %>%
gf_vline(xintercept = mean_diff_belief, colour = "red") %>%
gf_vline(xintercept = obs_diff_amas, colour = "purple") %>%
gf_refine(
scale_y_continuous(limits = c(0, 0.9), expand = c(0, 0)),
scale_x_continuous(
limits = c(-7.5, 7.5),
breaks = c(-10.0, -5.0, 0, 5, 10, obs_diff_amas),
labels = scales::number_format(
accuracy = 0.001,
decimal.mark = "."
)
)
) %>%
gf_annotate(
geom = "label", x = -4.5, y = 0.15,
label = "Sample-Difference Histogram and Density",
colour = "black"
) %>%
## Observed Difference
gf_annotate(
geom = "label", x = obs_diff_amas, y = 0.8,
label = "Observed Mean Difference", colour = "purple"
) %>%
## Null Hypothesis
gf_annotate(
geom = "label", x = mean_diff_belief, y = 0.7,
label = "Null Hypothesis (Belief)"
) %>%
## Confidence Intervals
gf_annotate("segment",
x = conf_int2$ci_low, y = 0.0,
xend = conf_int2$ci_low, yend = 0.5,
color = "purple", linewidth = 0.5
) %>%
gf_annotate("segment",
x = conf_int2$ci_high, y = 0.0,
xend = conf_int2$ci_high, yend = 0.5,
color = "purple", linewidth = 0.5
) %>%
gf_annotate("segment",
x = conf_int2$ci_low, y = 0.35,
xend = conf_int2$ci_high, yend = 0.35,
color = "purple", linewidth = 0.5,
arrow = arrow(length = unit(0.25, "cm"), ends = "both")
) %>%
gf_annotate(
geom = "label", x = obs_diff_amas, y = 0.4,
label = "95% Confidence Interval",
colour = "purple"
) %>%
gf_labs(
title = "Visualizing the t-test for Math Anxiety Scores",
subtitle = "Difference in Means, Confidence Intervals, and Test Statistic"
) %>%
gf_theme(theme_custom())We see that the difference between means is 3.2918431 times the std_error! At a distance of \(1.96\) (either way) the probability of this data happening by chance already drops to \(2.5 \%\) !! At this distance of 3.2918431, we would have negligible probability of this data occurring by chance!
All Tests Together
We can put all the test results together to get a few more insights about the tests:
Code
mosaic::t_test(AMAS ~ Gender,
data = MathAnxiety
) %>%
broom::tidy() %>%
kableExtra::kbl() %>%
kableExtra::kable_paper(full_width = F, html_font = "Roboto Condensed") %>%
kableExtra::column_spec(5, width = "20em", bold = T, background = "gold")
wilcox.test(AMAS ~ Gender,
data = MathAnxiety
) %>%
broom::tidy() %>%
kableExtra::kbl() %>%
kableExtra::kable_paper(full_width = F, html_font = "Roboto Condensed") %>%
kableExtra::column_spec(2, width = "10em", bold = T, background = "gold")
lm(AMAS ~ Gender,
data = MathAnxiety
) %>%
broom::tidy(
conf.int = TRUE,
conf.level = 0.95,
) %>%
kableExtra::kbl() %>%
kableExtra::kable_paper(full_width = F, html_font = "Roboto Condensed") %>%
kableExtra::column_spec(1, bold = T, border_right = T) %>%
kableExtra::column_spec(5, width = "10em", bold = T, background = "gold")
lm(rank(AMAS) ~ Gender,
data = MathAnxiety
) %>%
broom::tidy(
conf.int = TRUE,
conf.level = 0.95
) %>%
kableExtra::kbl() %>%
kableExtra::kable_paper(full_width = F, html_font = "Roboto Condensed") %>%
kableExtra::column_spec(1, bold = T, border_right = T) %>%
kableExtra::column_spec(5, width = "10em", bold = T, background = "gold")| estimate | estimate1 | estimate2 | statistic | p.value | parameter | conf.low | conf.high | method | alternative |
|---|---|---|---|---|---|---|---|---|---|
| -1.7676 | 21.16718 | 22.93478 | -3.291843 | 0.0010558 | 580.2004 | -2.822229 | -0.7129706 | Welch Two Sample t-test | two.sided |
| statistic | p.value | method | alternative |
|---|---|---|---|
| 37483 | 0.0007736 | Wilcoxon rank sum test with continuity correction | two.sided |
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | 21.16718 | 0.3641315 | 58.130602 | 0.0000000 | 20.4520482 | 21.882317 |
| GenderGirl | 1.76760 | 0.5364350 | 3.295087 | 0.0010422 | 0.7140708 | 2.821129 |
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | 278.04644 | 9.535561 | 29.158898 | 0.0000000 | 259.31912 | 296.7738 |
| GenderGirl | 47.64559 | 14.047696 | 3.391701 | 0.0007405 | 20.05668 | 75.2345 |
As we can see, all tests are in agreement that there is a significant effect of Gender on the AMAS anxiety scores!
We can use the visStatistics package to run all the tests in one go, using the in-built decision tree. This is a very useful package for teaching statistics, and it can be used to run all the tests we have seen so far, and more. Here goes: we use the visstat function to run all the tests, and then we can summarize the results. The visstat function takes a dataset, a quantitative variable, a qualitative variable, and some options for the tests to run.
From the visStatistics package documentation:
visStatistics automatically selects and visualises appropriate statistical hypothesis tests between two column vectors of type of class “numeric”, “integer”, or “factor”. The choice of test depends on the class, distribution, and sample size of the vectors, as well as the user-defined ‘conf.level’. The main function
visstat()visualises the selected test with appropriate graphs (box plots, bar charts, regression lines with confidence bands, mosaic plots, residual plots, Q-Q plots), annotated with the main test results, including any assumption checks and post-hoc analyses.
Summary of visstat object
--- Named components ---
[1] "dependent variable (response)" "independent variables (features)"
[3] "t-test-statistics" "Shapiro-Wilk-test_sample1"
[5] "Shapiro-Wilk-test_sample2"
--- Contents ---
$dependent variable (response):
[1] "AMAS"
$independent variables (features):
[1] Boy Girl
Levels: Boy Girl
$t-test-statistics:
Welch Two Sample t-test
data: x1 and x2
t = -3.2918, df = 580.2, p-value = 0.001056
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.8222293 -0.7129706
sample estimates:
mean of x mean of y
21.16718 22.93478
$Shapiro-Wilk-test_sample1:
Shapiro-Wilk normality test
data: x
W = 0.99043, p-value = 0.03343
$Shapiro-Wilk-test_sample2:
Shapiro-Wilk normality test
data: x
W = 0.99074, p-value = 0.07835
--- Attributes ---
$plot_paths
character(0)The tool runs the Welch t-test and declares the p-value to be significant. The Shapiro-Wilk test results here also confirm what we had performed earlier. Hence we can say that we may reject the NULL Hypothesis and state that there is a statistically significant difference in AMAS anxiety scores between Boys and Girls.
An AI Generated Explanation of the Statistical Model
We have used the statlingua package to generate an AI explanation of the statistical model t1_amas we have used in this module. statlingua interfaces to the ellmer package, which in turn interfaces to the ollama API for AI explanations. The AI model used is llama3.1, and the explanation is tailored for a novice audience with moderate verbosity.
AI Generated Explanation
The command was run in the Console and the results pasted into this Quarto document. I have not edited this at all. Do look for complex verbiage and outright hallucinatory responses.
Code
library(ellmer)
library(statlingua)
library(chores)
client <- ellmer::chat_ollama(model = "llama3.1", echo = FALSE)
###
exam_context <- "
The model uses a data set on child Math-related Anxiety scores from the resampledata package in R. The dataset has Age, Gender, Grade, and Arithmeitc test score variables, along with AMS and RCMAS math-anxiety scores.
The hypothesis is that the average Math Anxiety score is no different for Boys and Girls. The model conducted is a two-sample t-test to assess whether the mean of the Math Anxiety scores significantly differ between Boys and Girls."
explanation_amas <- statlingua::explain(t1_amas,
client = client,
context = exam_context,
audience = "novice", verbosity = "moderate"
) # moderate / detailedWelch Two Sample t-test Output Explanation
The output given represents the results from conducting a Welch Two Sample t-test on the AMAS (Math-Related Anxiety Scale) variable in the dataset, specifically examining differences in mean anxiety scores between boys (Boy) and girls (Girl).
Assumptions and Suitability
Given context, the hypothesis to be tested is that average Math Anxiety scores are no different for Boys and Girls. A Welch Two Sample t-test is chosen, suitable given its independence of observations assumption aligned with the stated dataset properties.
It assumes data follows a normal distribution in each group, though the test itself does not check for normality. However, due to non-homogeneous variance typical in many datasets, a t-test variant specifically designed for such cases, like Welch’s, is preferable over the (more restrictive) homoscedastic t-test.
Output Components
- data:
AMAS by Gender- This indicates that the analysis comparing means of Math anxiety scores (AMAS) between genders (BoyandGirl) generated this output. - Test Statistic: The calculated test statistic is
t = -3.2918. A negative t-value suggests an average math-anxiety-score difference in a direction favoring girls (higher average score for them), compared to boys. - Degrees of Freedom (
df): The degrees of freedom associated with this test aredf = 580.2. This value is not an integer, which is typical for Welch’s t-test due to its handling of unequal variances among the groups. - p-value: The p-value from the output,
0.001056, is considered highly significant at any conventional significance level (e.g., \(\alpha = 0.05\)). This implies the average Math Anxiety score significantly differs between boys and girls according to the test. - Alternative Hypothesis: This output supports an alternative hypothesis stating that true differences in means (
true difference in means between group Boy and group Girl is not equal to 0). From the research question’s perspective, this confirms that there are significant differing mean Math Anxiety scores for boys and girls. - 95% Confidence Interval (CI): Provided a confidence interval which suggests with 95% confidence, the population average math anxiety score difference can fall between
-2.8222293and-0.7129706. Since zero is within this range, one might initially question the interpretation of significant differences based on p-values alone. Hallucination!!! - Sample Estimates: Offers summary statistics (means) for individual groups (
mean in group Boy = 21.16718,mean in group Girl = 22.93478), highlighting the observed average Math Anxiety scores per gender.
Checking Assumptions and Practical Suggestions
Given this analysis, practical steps to check assumptions include: - Normality of Data: Assess using graphical methods (histograms, Q-Q plots for each group). Check with Shapiro-Wilk test.
If data shows clear indication against normality or from formal tests (e.g., Shapiro-Wilk W-statistic indicates distribution significantly deviates from being normally distributed), consider a non-parametric alternative.
- Equal Variance Assumption: Since the Welch variant was used here, assessing equal variances isn’t directly necessary with its output. But to check formally, one might use Levene’s Test or Barlett’s test, and if significant, reconsider using Welch’s for a better estimate of effects in such scenarios.
Conclusion
At \(\alpha = 0.001056\), the observed differences (higher mean Math Anxiety among girls than boys) are considered statistically significant. Therefore, based on this analysis and context provided, we have sufficient evidence to reject the null hypothesis that there is no difference in average Math-related Anxiety Scores between boys and girls.
Every two years, the Centers for Disease Control and Prevention in the USA conduct the Youth Risk Behavior Surveillance System (YRBSS) survey, where it takes data from high-schoolers (9th through 12th grade), to analyze health patterns. We will work with a selected group of variables from a random sample of observations during one of the years the YRBSS was conducted. The yrbss dataset is part of the openintro package. Type this in your console: help(yrbss).
We have 13K data entries, and with 13 different variables, some Qual and some Quant. Many entries are missing too, typical of real-world data and something we will have to account for in our computations. The meaning of each variable can be found by bringing up the help file. Type help(yrbss) in your Console.
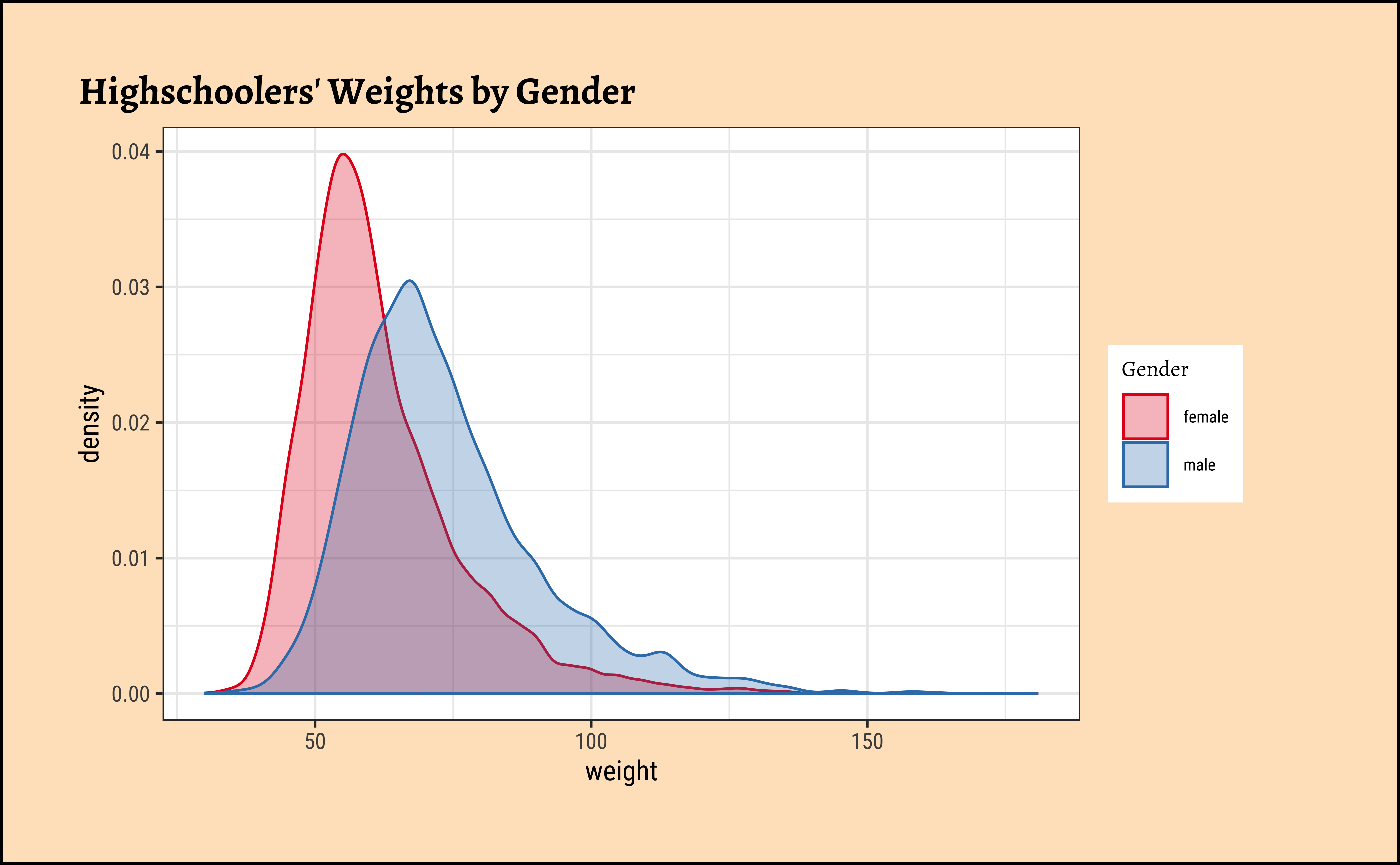
First, histograms, densities and counts of the variable we are interested in:
Code
ggplot2::theme_set(new = theme_custom())
yrbss_select_gender %>%
gf_density(~weight,
fill = ~gender, colour = ~gender,
alpha = 0.3,
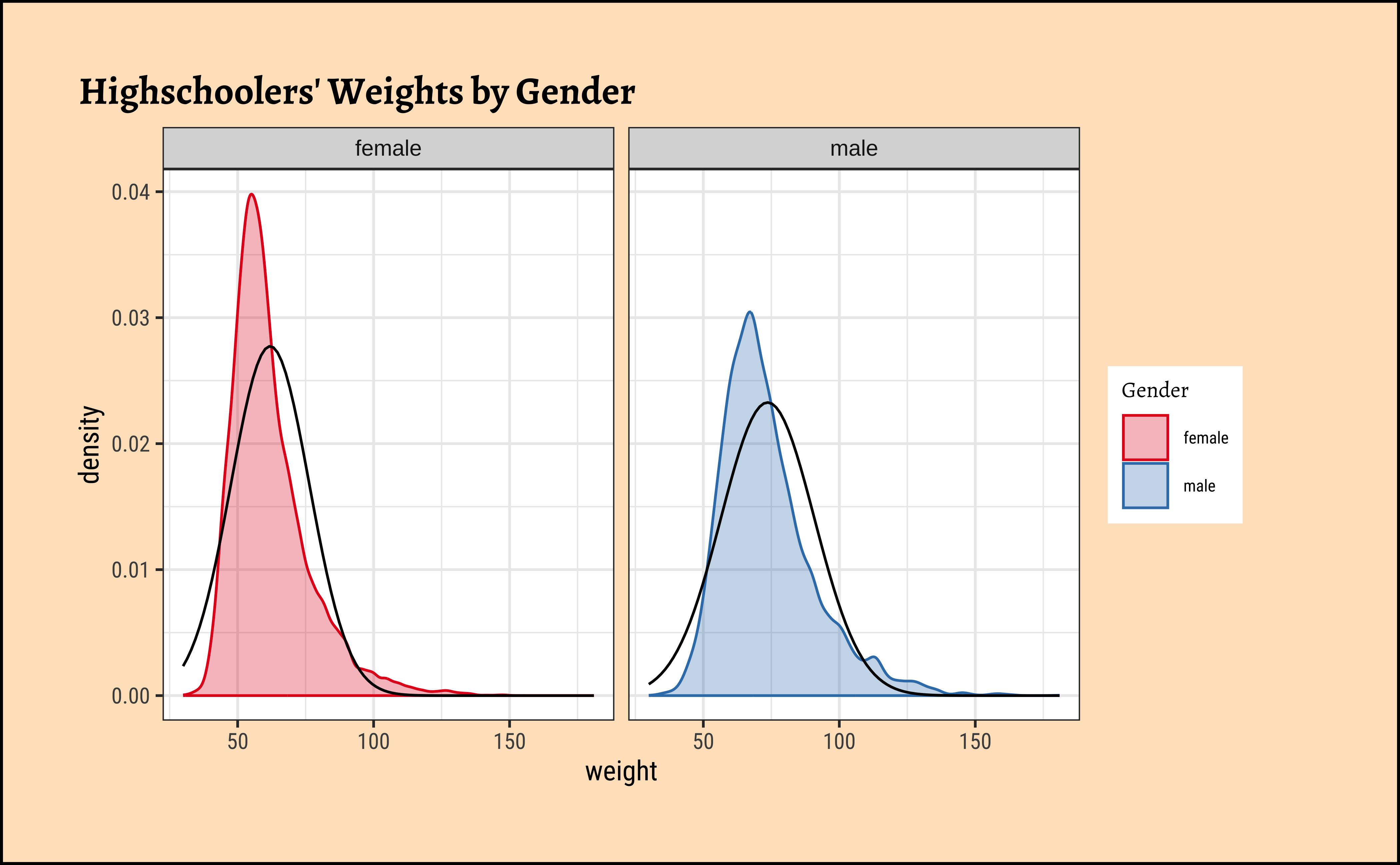
title = "Highschoolers' Weights by Gender"
) %>%
gf_refine(scale_fill_brewer(
name = "Gender", palette = "Set1",
aesthetics = c("colour", "fill")
))
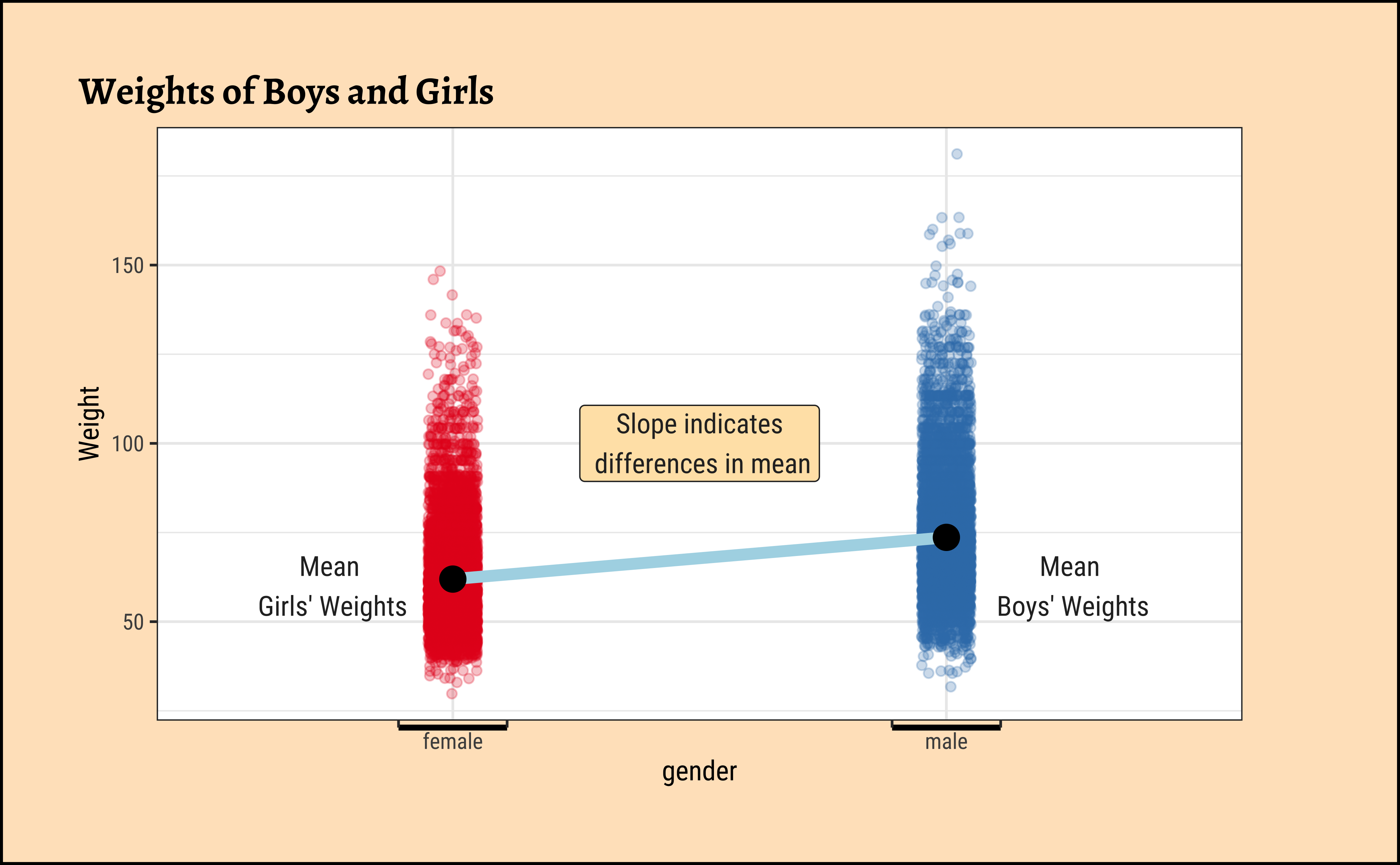
###
yrbss_select_gender %>%
gf_jitter(weight ~ gender,
color = ~gender,
show.legend = FALSE,
width = 0.05, alpha = 0.25,
ylab = "Weight",
title = "Weights of Boys and Girls"
) %>%
gf_summary(
group = ~1, # See the reference link above. Damn!!!
fun = "mean", geom = "line", colour = "lightblue",
lty = 1, linewidth = 2
) %>%
gf_summary(
fun = "mean", colour = "black",
size = 4, geom = "point"
) %>%
gf_refine(scale_x_discrete(
breaks = c("male", "female"),
labels = c("male", "female"),
guide = guide_prism_bracket(width = 0.1, outside = FALSE)
)) %>%
gf_annotate(
x = 0.75, y = 60, geom = "text",
label = "Mean\n Girls' Weights"
) %>%
gf_annotate(
x = 2.25, y = 60, geom = "text",
label = "Mean\n Boys' Weights"
) %>%
gf_annotate(
x = 1.5, y = 100, geom = "label",
label = "Slope indicates\n differences in mean",
fill = "moccasin"
) %>%
gf_refine(scale_colour_brewer(name = "Gender", palette = "Set1")) %>%
gf_theme(theme(legend.position = "none", axis.line.x = element_line(linewidth = 1)))Overlapped Distribution plot shows some difference in the means; and the Jitter plots show visible difference in the means. In this Case Study, our research question is:
Research Question
Does weight of highschoolers in this dataset vary with gender?
Based on the graphs, how would we formulate our Hypothesis? We wish to infer whether there is difference in mean weight across gender. So accordingly:
\[ H_0: \mu_{weight-male} = \mu_{weight-female} \]
\[ H_a: \mu_{weight-male} \ne \mu_{weight-female} \]
A.
As stated before, statistical tests for means usually require a couple of checks:
- Are the data normally distributed?
- Are the data variances similar?
We will complete a visual check for normality with plots, and since we cannot do a shapiro.test (length(data) >= 5000) we can use the Anderson-Darling test.
Let us plot frequency distribution and Q-Q plots1 for both variables.
Code
ggplot2::theme_set(new = theme_custom())
male_student_weights <- yrbss_select_gender %>%
filter(gender == "male") %>%
select(weight)
##
female_student_weights <- yrbss_select_gender %>%
filter(gender == "female") %>%
select(weight)
# shapiro.test(male_student_weights$weight)
# shapiro.test(female_student_weights$weight)
yrbss_select_gender %>%
gf_density(~weight,
fill = ~gender, colour = ~gender,
alpha = 0.3,
title = "Highschoolers' Weights by Gender"
) %>%
gf_facet_grid(~gender) %>%
gf_fitdistr(dist = "dnorm") %>%
gf_refine(scale_fill_brewer(name = "Gender", palette = "Set1", aesthetics = c("colour", "fill")))
##
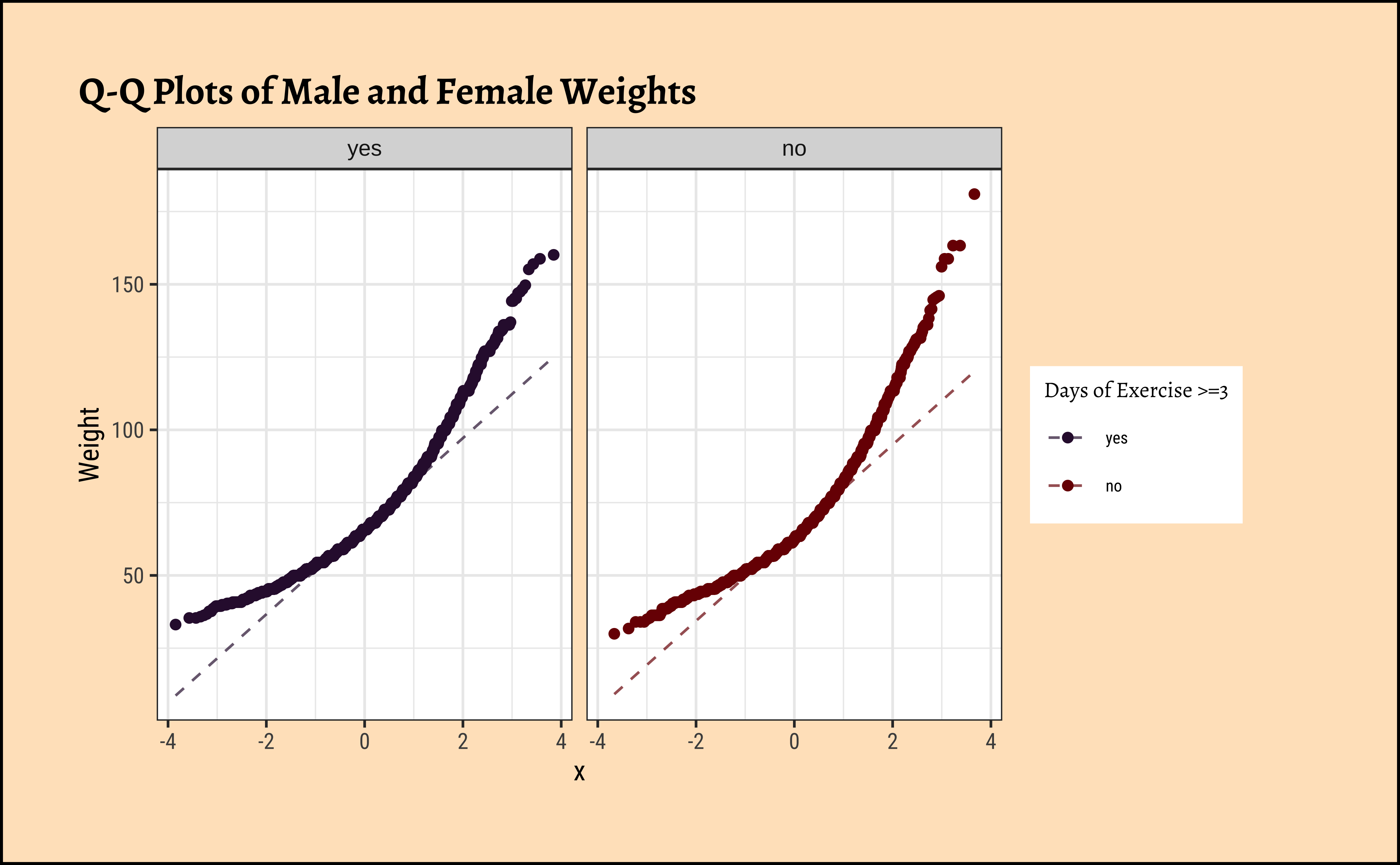
yrbss_select_gender %>%
gf_qqline(~ weight | gender, ylab = "weight", colour = ~gender) %>%
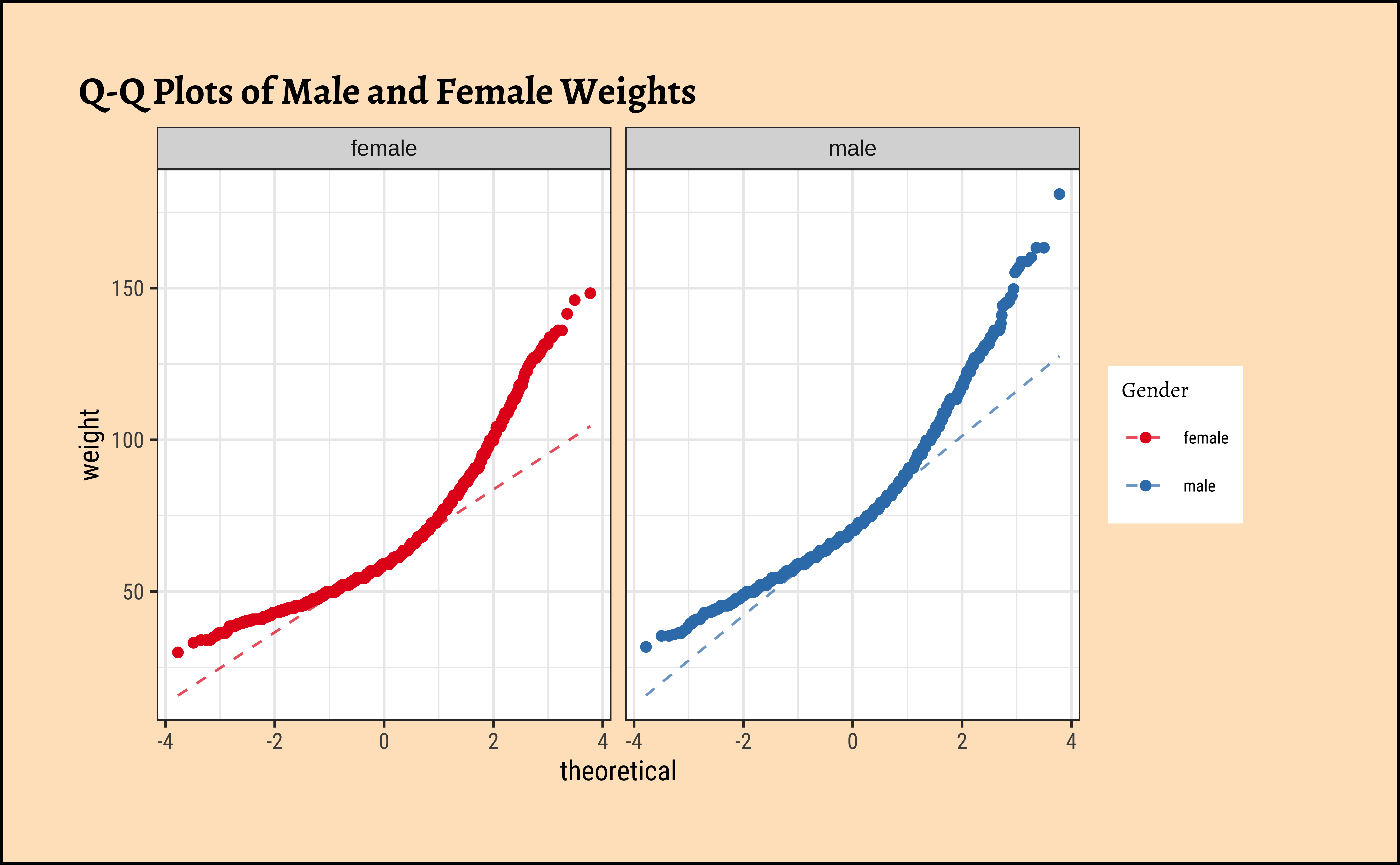
gf_qq(title = "Q-Q Plots of Male and Female Weights") %>%
gf_refine(scale_fill_brewer(name = "Gender", palette = "Set1", aesthetics = c("colour", "fill")))Distributions are not too close to normal…perhaps a hint of a rightward skew, suggesting that there are some obese students.
No real evidence (visually) of the variables being normally distributed.
Anderson-Darling normality test
data: male_student_weights$weight
A = 113.23, p-value < 2.2e-16
Anderson-Darling normality test
data: female_student_weights$weight
A = 157.17, p-value < 2.2e-16p-values are very low and there is no reason to think that the data is normal.
B.
Let us check if the two variables have similar variances: the var.testdoes this for us, with a NULL hypothesis that the variances are not significantly different:
The p.value being so small, we are able to reject the NULL Hypothesis that the variances of weight are nearly equal across the two exercise regimes.
Conditions
- The two variables are not normally distributed.
- The two variances are also significantly different.
This means that the parametric t.test must be eschewed in favour of the non-parametric wilcox.test. We will use that, and also attempt linear models with rank data, and a final permutation test.
What would be the test statistic we would use? The difference in means. Is the observed difference in the means between the two groups of scores non-zero? We use the diffmean function, from mosaic:
diffmean
11.70089
Since the data variables do not satisfy the assumption of being normally distributed, and the variances are significantly different, we use the classical wilcox.test, which implements what we need here: the Mann-Whitney U test,
Our model would be:
\[ mean(rank(Weight_{male})) - mean(rank(Weight_{female})) = \beta_1; \]
\[ H_0: \mu_{weight-male} = \mu_{weight-female} \]
\[ H_a: \mu_{weight-male} \ne \mu_{weight-female} \]
Recall the earlier graph showing ranks of anxiety-scores against Gender.
The p.value is negligible and we are able to reject the NULL hypothesis that the means are equal.
We can apply the linear-model-as-inference interpretation to the ranked data data to implement the non-parametric test as a Linear Model:
\[ lm(rank(weight) \sim gender) = \beta_0 + \beta_1 * gender \]
\[ H_0: \beta_1 = 0 \]
\[ H_a: \beta_1 \ne 0\\ \]
Dummy Variables in lm
Note how the Qual variable was used here in Linear Regression lm()! The gender variable was treated as a binary “dummy” variable1.
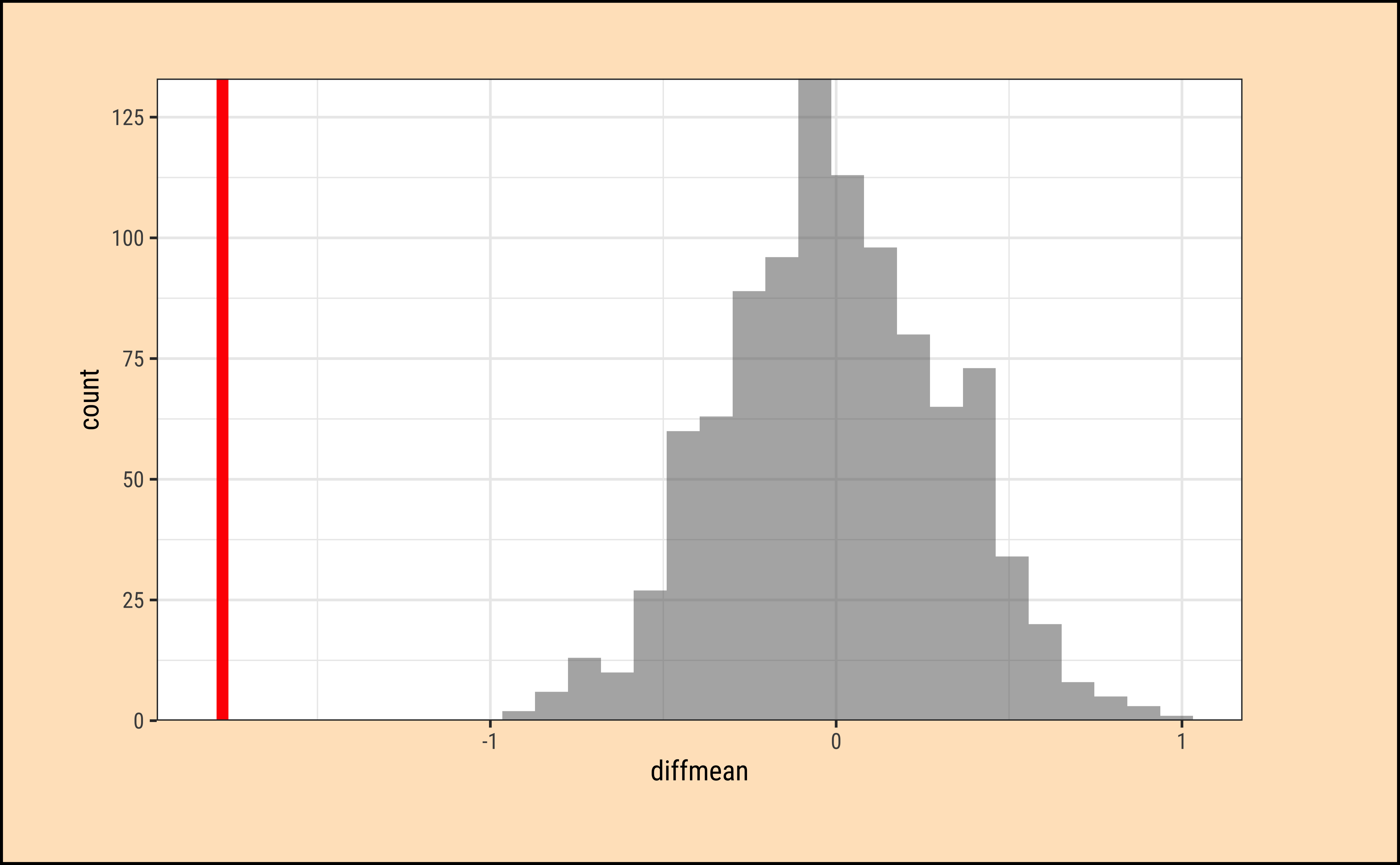
For the specific data at hand, we need to shuffle the gender and take the test statistic (difference in means) each time.
Code
ggplot2::theme_set(new = theme_custom())
null_dist_weight <-
do(4999) * diffmean(
data = yrbss_select_gender,
weight ~ shuffle(gender)
)
null_dist_weight
###
prop1(~ diffmean <= obs_diff_gender, data = null_dist_weight)
###
gf_histogram(
data = null_dist_weight, ~diffmean,
bins = 25
) %>%
gf_vline(
xintercept = obs_diff_gender,
colour = "red", linewidth = 1,
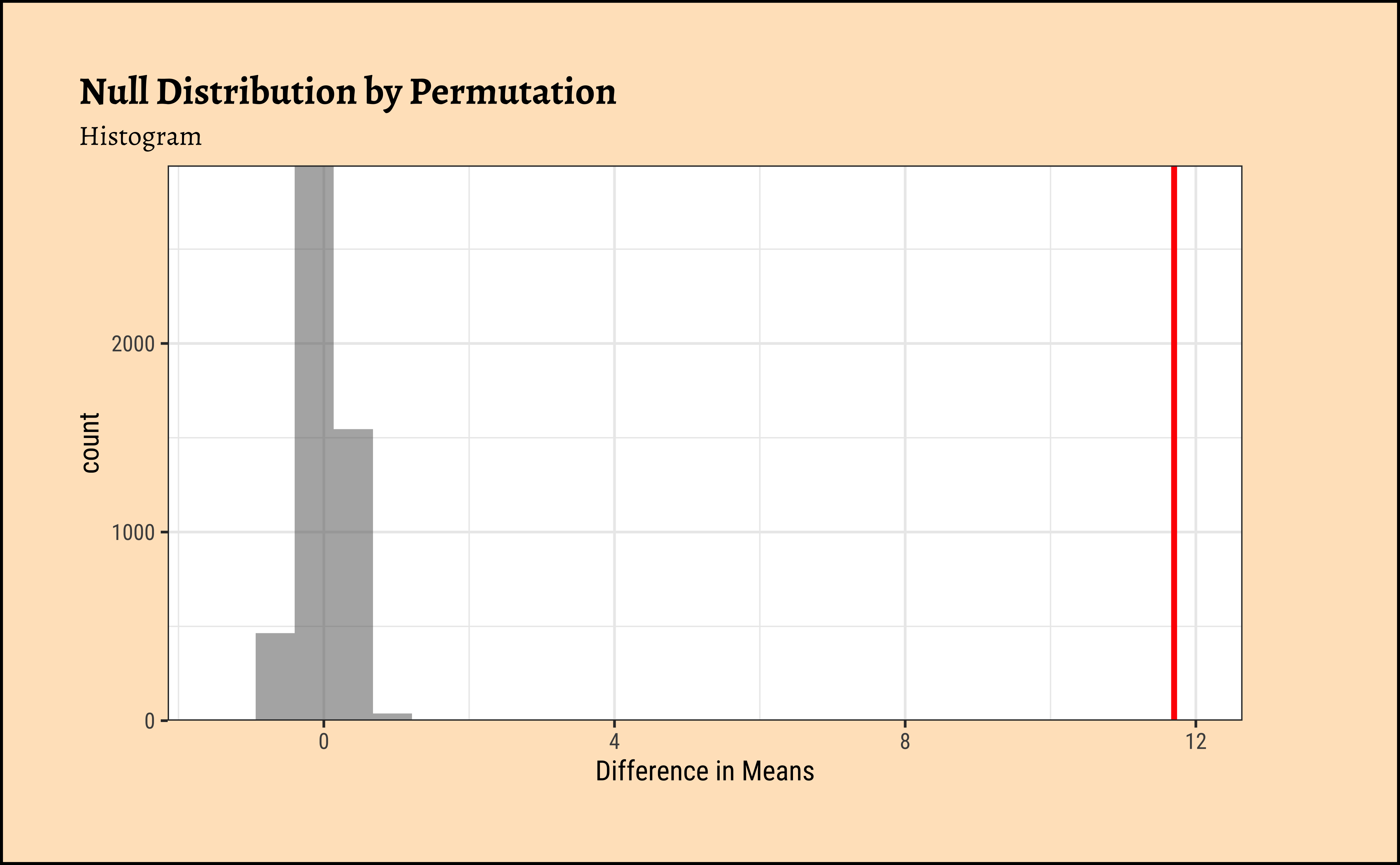
title = "Null Distribution by Permutation",
subtitle = "Histogram"
) %>%
gf_labs(x = "Difference in Means") %>%
gf_refine(scale_y_continuous(expand = c(0, 0)))
###
gf_ecdf(
data = null_dist_weight, ~diffmean,
linewidth = 1
) %>%
gf_vline(
xintercept = obs_diff_gender,
colour = "red", linewidth = 1,
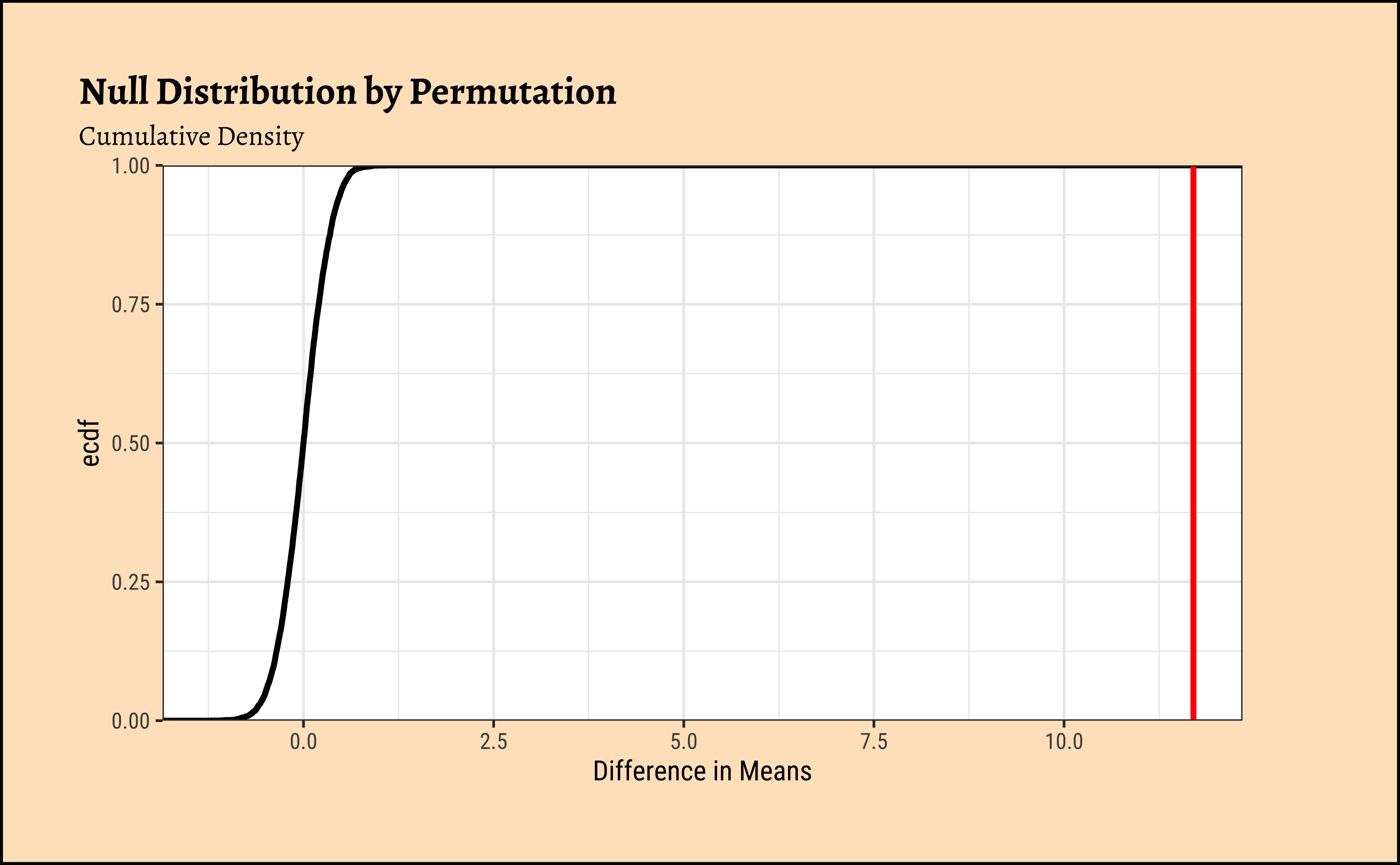
title = "Null Distribution by Permutation",
subtitle = "Cumulative Density"
) %>%
gf_labs(x = "Difference in Means") %>%
gf_refine(scale_y_continuous(expand = c(0, 0)))prop_TRUE
1 Clearly the observed_diff_weight is much beyond anything we can generate with permutations with gender! And hence there is a significant difference in weights across gender!
All Tests Together
We can put all the test results together to get a few more insights about the tests:
Code
wilcox.test(weight ~ gender,
data = yrbss_select_gender,
conf.int = TRUE,
conf.level = 0.95
) %>%
broom::tidy() %>%
tt() %>%
style_tt(i = 1, j = 3, background = "gold", color = "black")
lm(rank(weight) ~ gender,
data = yrbss_select_gender
) %>%
broom::tidy(
conf.int = TRUE,
conf.level = 0.95
) %>%
tt() %>%
style_tt(i = 1, j = 5, background = "gold", color = "black")| estimate | statistic | p.value | conf.low | conf.high | method | alternative |
|---|---|---|---|---|---|---|
| -11 | 10808212 | 0 | -11 | -11 | Wilcoxon rank sum test with continuity correction | two.sided |
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | 4836 | 43 | 114 | 0 | 4753 | 4920 |
| gendermale | 2851 | 60 | 48 | 0 | 2735 | 2968 |
The wilcox.test and the linear model with rank data offer the same results. This is of course not surprising!
We need to use a smaller sample of the dataset yrbss_select_gender, for the (same) reason: visstat() defaults to using the shapiro.wilk test internally:
Summary of visstat object
--- Named components ---
[1] "dependent variable (response)" "independent variables (features)"
[3] "t-test-statistics" "Shapiro-Wilk-test_sample1"
[5] "Shapiro-Wilk-test_sample2"
--- Contents ---
$dependent variable (response):
[1] "weight"
$independent variables (features):
[1] male female
Levels: female male
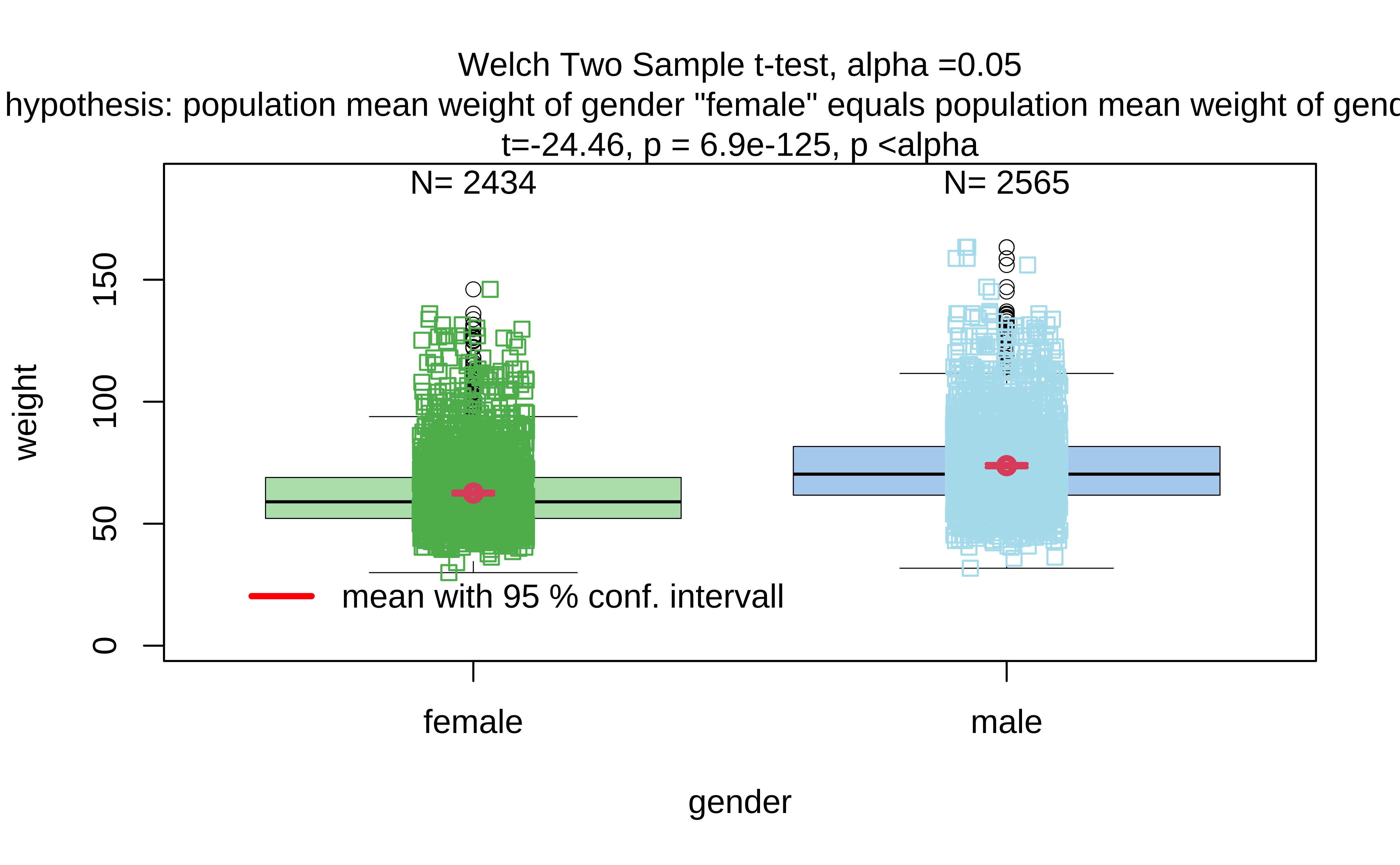
$t-test-statistics:
Welch Two Sample t-test
data: x1 and x2
t = -24.465, df = 4954.8, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-12.14354 -10.34172
sample estimates:
mean of x mean of y
62.54529 73.78792
$Shapiro-Wilk-test_sample1:
Shapiro-Wilk normality test
data: x
W = 0.88612, p-value < 2.2e-16
$Shapiro-Wilk-test_sample2:
Shapiro-Wilk normality test
data: x
W = 0.93065, p-value < 2.2e-16
--- Attributes ---
$plot_paths
character(0)Compare these results with those calculated earlier!
Finally, consider the possible relationship between a highschooler’s weight and their physical activity.
First, let’s create a new variable physical_3plus, which will be coded as either “yes” if the student is physically active for at least 3 days a week, and “no” if not. Recall that we have several missing data in that column, so we will (sadly) drop these before generating the new variable:
yrbss_select_phy <- yrbss %>%
drop_na(physically_active_7d, weight) %>%
## add new variable physical_3plus
mutate(
physical_3plus = if_else(physically_active_7d >= 3,
"yes", "no"
),
# Convert it to a factor Y/N
physical_3plus = factor(physical_3plus,
labels = c("yes", "no"),
levels = c("yes", "no")
)
) %>%
select(weight, physical_3plus)
# Let us check
yrbss_select_phy %>% count(physical_3plus)Research Question
Does weight vary based on whether students exercise on more or less than 3 days a week? (physically_active_7d >= 3 days)
We can make distribution plots for weight by physical_3plus:
Code
ggplot2::theme_set(new = theme_custom())
###
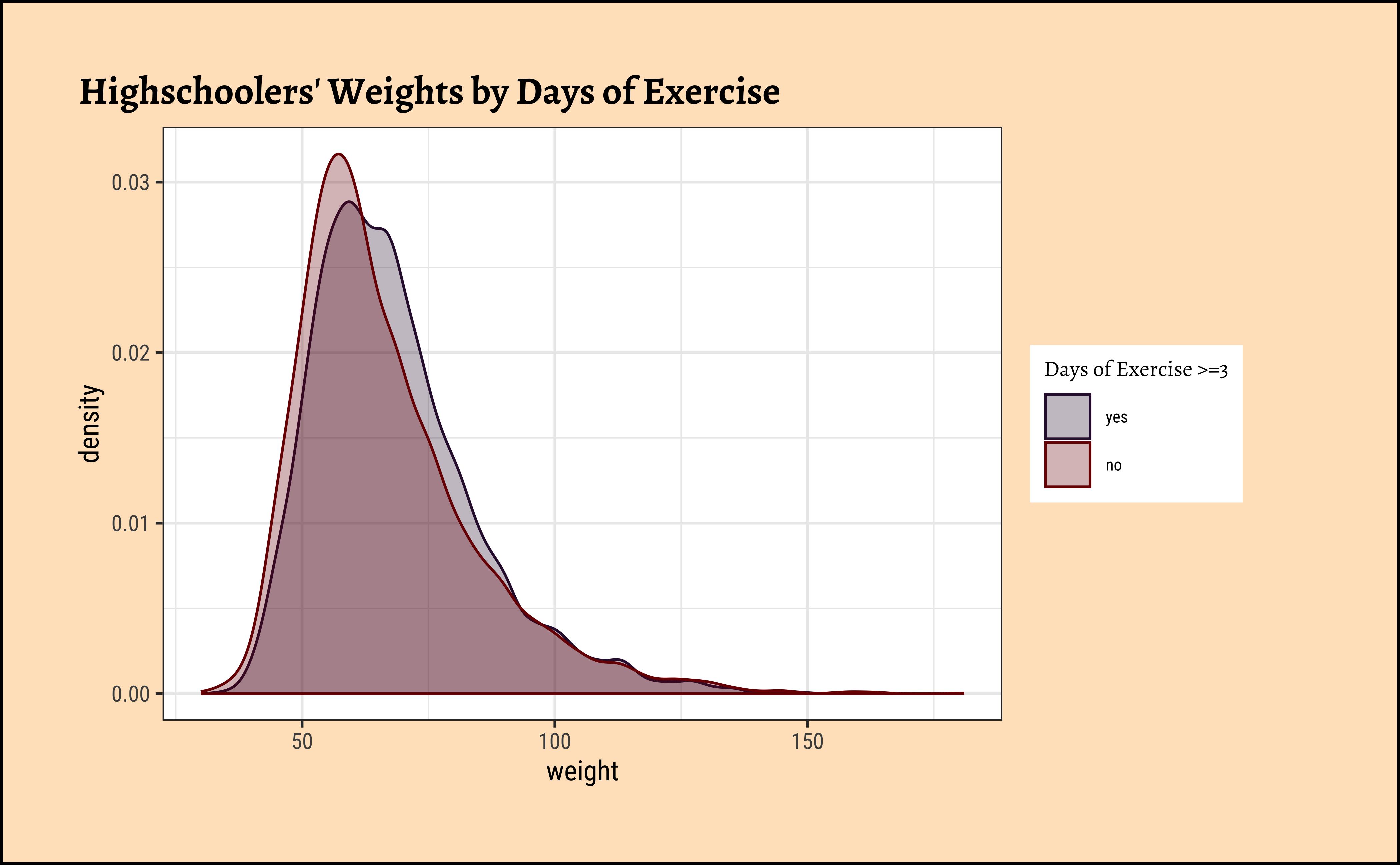
gf_density(~weight,
fill = ~physical_3plus, colour = ~physical_3plus,
data = yrbss_select_phy, alpha = 0.3,
title = "Highschoolers' Weights by Days of Exercise"
) %>%
gf_refine(scale_fill_viridis_d(
name = "Days of Exercise >=3",
option = "turbo",
aesthetics = c("colour", "fill")
))
##
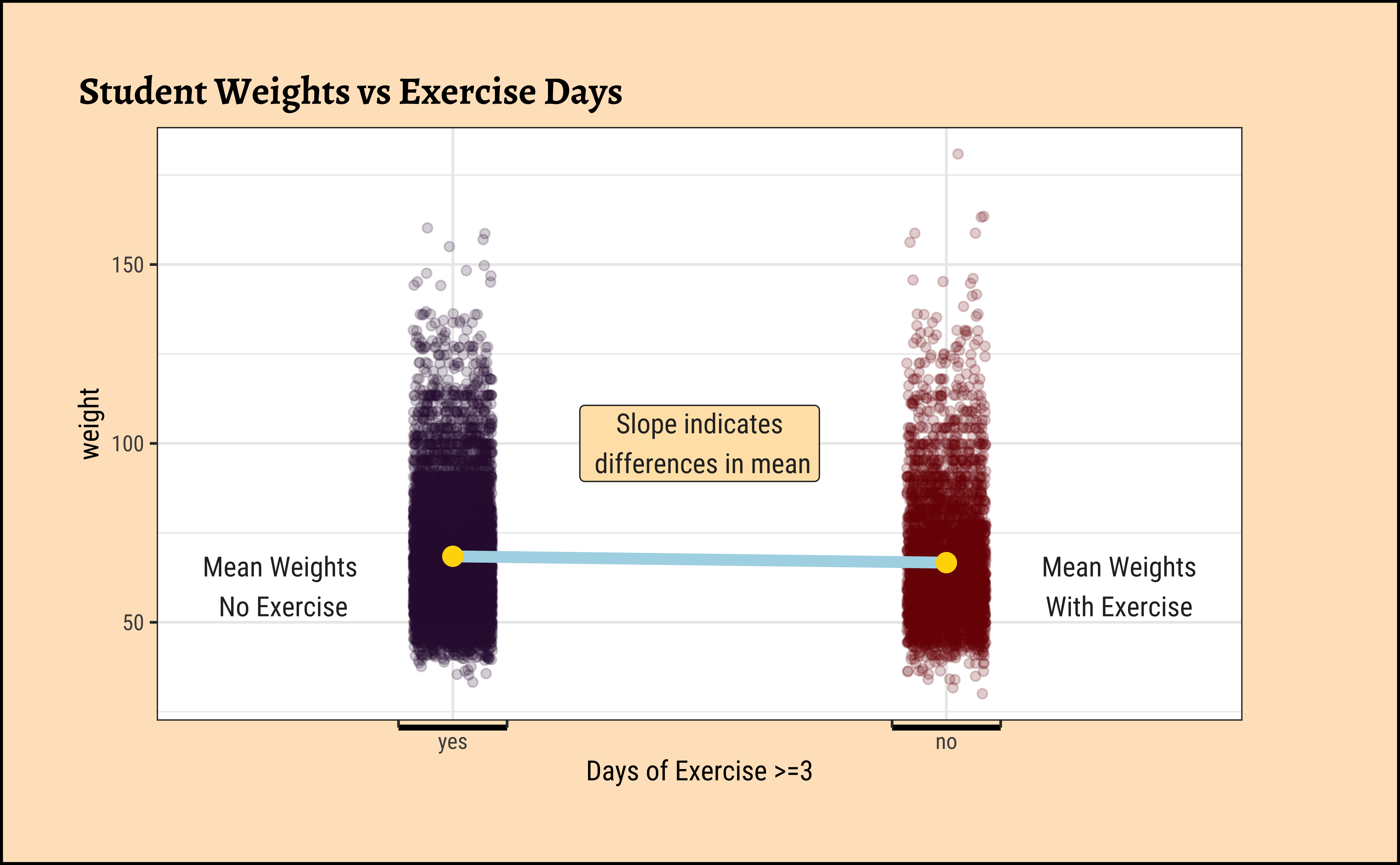
yrbss_select_phy %>%
gf_jitter(weight ~ physical_3plus,
colour = ~physical_3plus,
width = 0.08, alpha = 0.2,
xlab = "Days of Exercise >=3",
title = "Student Weights vs Exercise Days"
) %>%
gf_summary(
group = ~1, # See the reference link above. Damn!!!
fun = "mean", geom = "line", colour = "lightblue",
lty = 1, linewidth = 2
) %>%
gf_summary(fun = "mean", geom = "point", size = 3, colour = "gold") %>%
gf_refine(scale_x_discrete(
breaks = c("no", "yes"),
labels = c("no", "yes"),
guide = guide_prism_bracket(width = 0.1, outside = FALSE)
)) %>%
gf_refine(
annotate(x = 0.65, y = 60, geom = "text", label = "Mean Weights\n No Exercise"),
annotate(x = 2.35, y = 60, geom = "text", label = "Mean Weights\nWith Exercise"),
annotate(x = 1.5, y = 100, geom = "label", label = "Slope indicates\n differences in mean", fill = "moccasin"),
scale_colour_viridis_d(name = "Days of Exercise >=3", option = "turbo")
) %>%
gf_theme(theme(legend.position = "none", axis.line.x = element_line(linewidth = 1)))The jitter and density plots show the comparison between the two means. We can also compare the means of the distributions using the following to first group the data by the physical_3plus variable, and then calculate the mean weight in these groups using the mean function while ignoring missing values by setting the na.rm argument to TRUE.
There is an observed difference, but is this difference large enough to deem it “statistically significant”? In order to answer this question we will conduct a hypothesis test. But before that a few more checks on the data:
A.
As stated before, statistical tests for means usually require a couple of checks:
- Are the data normally distributed?
- Are the data variances similar?
Let us also complete a visual check for normality,with plots since we cannot do a shapiro.test:
Code
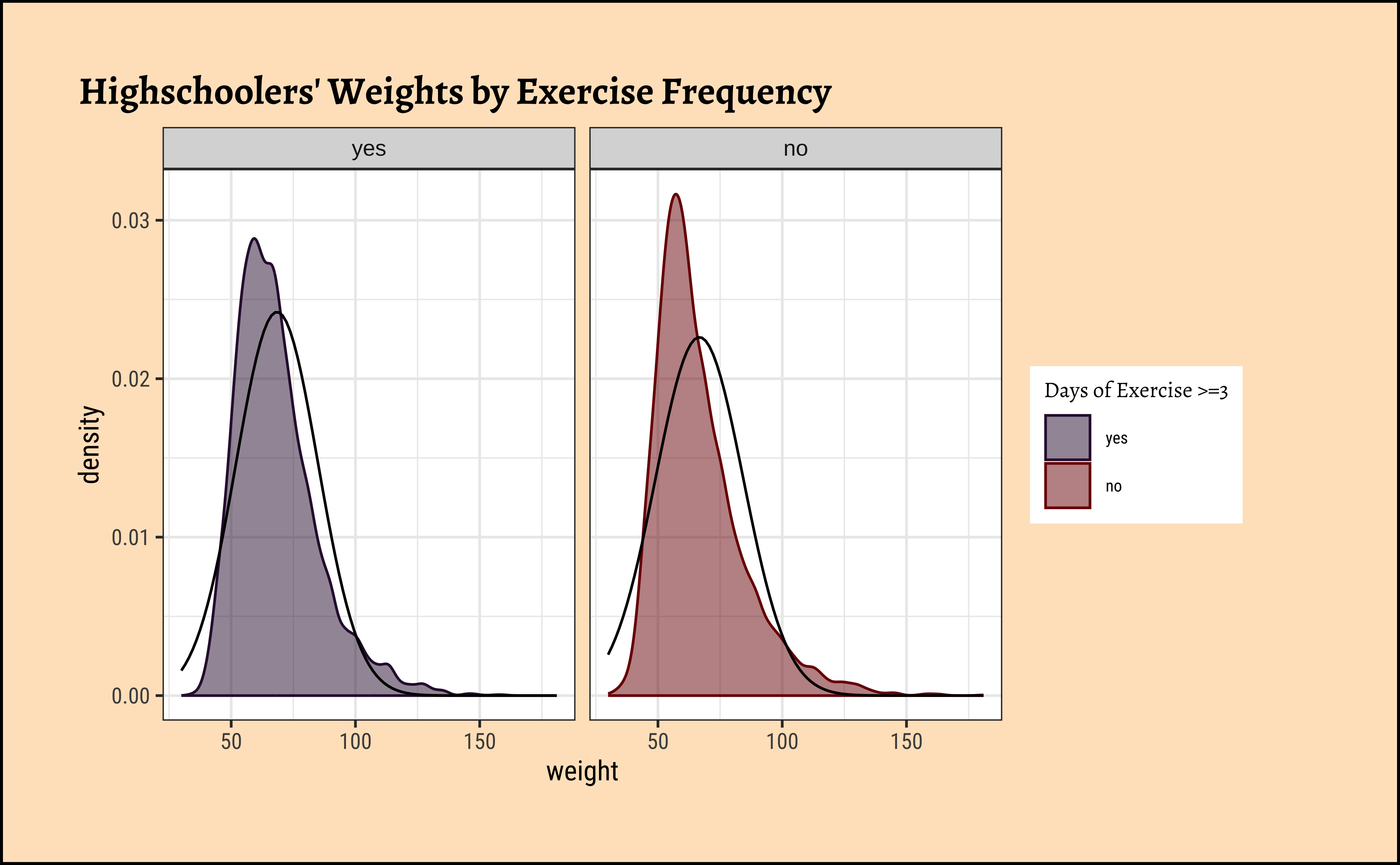
ggplot2::theme_set(new = theme_custom())
yrbss_select_phy %>%
gf_density(~weight,
fill = ~physical_3plus, color = ~physical_3plus,
alpha = 0.5,
title = "Highschoolers' Weights by Exercise Frequency"
) %>%
gf_facet_grid(~physical_3plus) %>%
gf_fitdistr(dist = "dnorm") %>%
gf_refine(scale_fill_viridis_d(
name = "Days of Exercise >=3",
option = "turbo",
aesthetics = c("colour", "fill")
))
##
yrbss_select_phy %>%
gf_qq(~ weight | physical_3plus,
color = ~physical_3plus,
title = "Q-Q Plots of Male and Female Weights"
) %>%
gf_qqline(ylab = "Weight") %>%
gf_refine(scale_fill_viridis_d(
name = "Days of Exercise >=3",
option = "turbo",
aesthetics = c("colour", "fill")
))Again, not normally distributed…
B.
Let us check if the two variables have similar variances: the var.test does this for us, with a NULL hypothesis that the variances are not significantly different:
[1] 1.054398The p.value states the probability of the data being what it is, assuming the NULL hypothesis that variances were similar. It being so small, we are able to reject this NULL Hypothesis that the variances of weight are nearly equal across the two exercise frequencies. (Compare the statistic in the var.test with the critical F-value)
Conditions
- The two variables are not normally distributed.
- The two variances are also significantly different.
Hence we will have to use non-parametric tests to infer if the means are similar.
Based on the graphs, how would we formulate our Hypothesis? We wish to infer whether there is difference in mean weight across physical_3plus. So accordingly:
\[ H_0: \mu_{physical-3plus-Yes} = \mu_{physical-3plus-No} \]
\[ H_a: \mu_{physical-3plus-Yes} \ne \mu_{physical-3plus-No} \]
What would be the test statistic we would use? The difference in means. Is the observed difference in the means between the two groups of scores non-zero? We use the diffmean function, from mosaic:
diffmean
-1.774584
Well, the variables are not normally distributed, and the variances are significantly different so a standard t.test is not advised. We can still try:
The p.value is \(8.9e-08\) ! And the Confidence Interval is clear of \(0\). So the t.test gives us good reason to reject the Null Hypothesis that the means are similar. But can we really believe this, given the non-normality of data?
However, we have seen that the data variables are not normally distributed. So a non-parametric Wilcoxon Test, using signed-ranks, is indicated: (recall the model!)
# For stability reasons, it may be advisable to use rounded data or to set digits.rank = 7, say,
# such that determination of ties does not depend on very small numeric differences (see the example).
wilcox.test(weight ~ physical_3plus,
conf.int = TRUE,
conf.level = 0.95,
data = yrbss_select_phy
) %>%
broom::tidy()The nonparametric wilcox.test also suggests that the means for weight across physical_3plus are significantly different.
We can apply the linear-model-as-inference interpretation to the ranked data data to implement the non-parametric test as a Linear Model:
\[ lm(rank(weight) \sim physical.3plus) = \beta_0 + \beta_1 \times physical.3plus \\ H_0: \beta_1 = 0\\ \\\ H_a: \beta_1 \ne 0\\ \]
Here too, the linear model using rank data arrives at a conclusion similar to that of the Mann-Whitney U test.
Permutation Tests
For this last Case Study, we will do this in two ways, just for fun: one using our familiar mosaic package, and the other using the package infer.
But first, we need to initialize the test, which we will save as obs_diff_**.
diffmean
-1.774584 diffmean
-1.774584 Important
Note that obs_diff_infer is a 1 X 1 dataframe; obs_diff_mosaic is a scalar!!
Next, we will work through creating a permutation distribution using tools from the infer package.
In infer, the specify() function is used to specify the variables you are considering (notated y ~ x), and you can use the calculate() function to specify the statistic you want to calculate and the order of subtraction you want to use. For this hypothesis, the statistic you are searching for is the difference in means, with the order being yes - no.
After you have calculated your observed statistic, you need to create a permutation distribution. This is the distribution that is created by shuffling the observed weights into new physical_3plus groups, labeled “yes” and “no”.
We will save the permutation distribution as null_dist.
The hypothesize() function is used to declare what the null hypothesis is. Here, we are assuming that student’s weight is independent of whether they exercise at least 3 days or not.
We should also note that the type argument within generate() is set to "permute". This ensures that the statistics calculated by the calculate() function come from a reshuffling of the data (not a resampling of the data)! Finally, the specify() and calculate() steps should look familiar, since they are the same as what we used to find the observed difference in means!
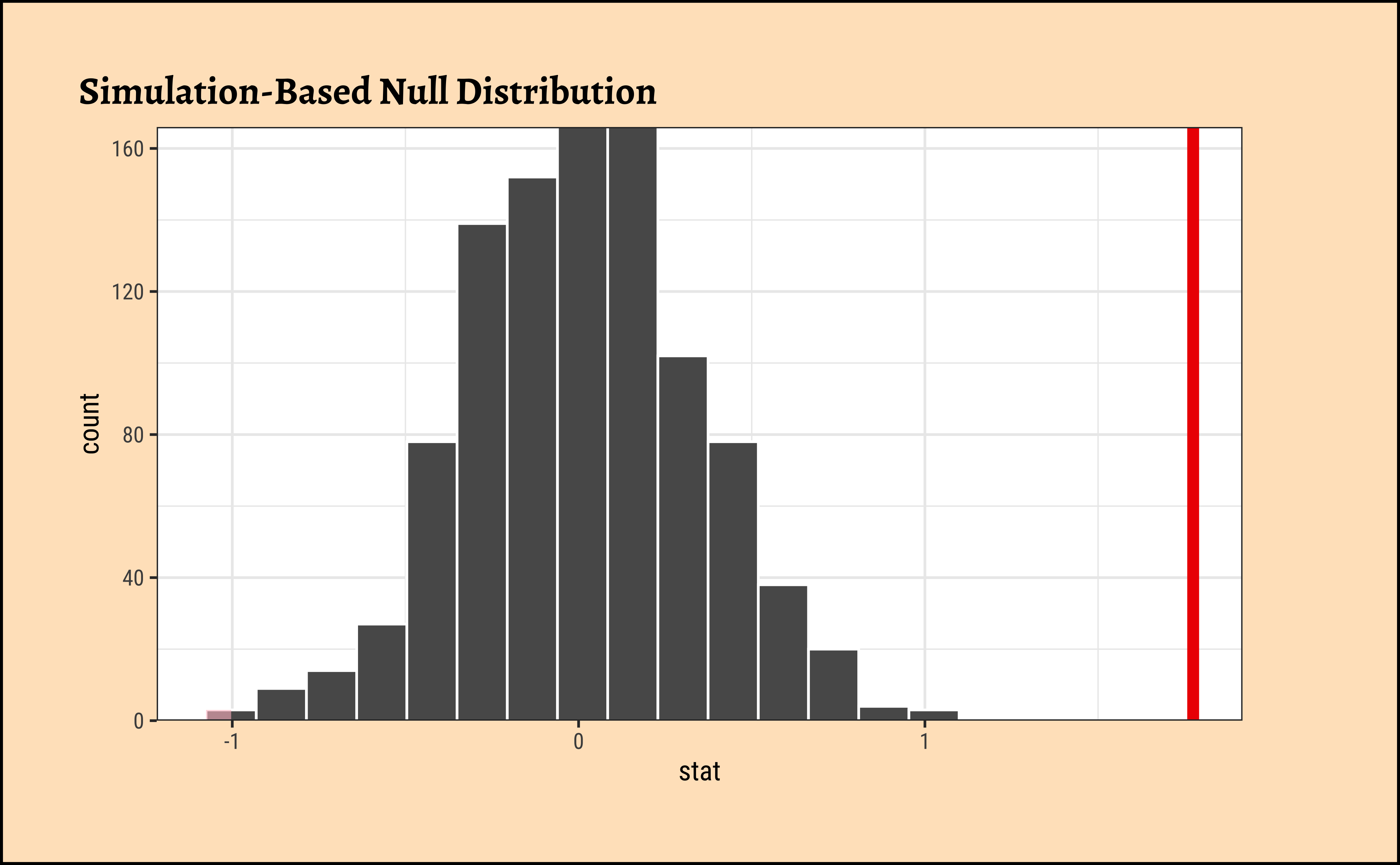
We can visualize this null distribution with the following code:
Code
Now that you have calculated the observed statistic and generated a permutation distribution, you can calculate the p-value for your hypothesis test using the function get_p_value() from the infer package.
What warning message do you get? Why do you think you get this warning message? Let us construct and record a confidence interval for the difference between the weights of those who exercise at least three times a week and those who don’t, and interpret this interval in context of the data.
It does look like the observed_diff_infer is too far away from this confidence interval. Hence if there was no difference in weight caused by physical_3plus, we would never have observed it! Hence the physical_3plus does have an effect on weight!
We already have the observed difference, obs_diff_mosaic. Now we generate the null distribution using permutation, with mosaic:
We can also generate the histogram of the null distribution, compare that with the observed diffrence and compute the p-value and confidence intervals:
Code
prop_TRUE
1 Again, it does look like the observed_diff_infer is too far away from this NULL distribution. Hence if there was no difference in weight caused by physical_3plus, we would never have observed it! Hence the physical_3plus does have an effect on weight!
Clearly there is a serious effect of Physical Exercise on the body weights of students in the population from which this dataset is drawn.
- In our target population for our design intervention, we often perceive groups
- We need often to infer differences in some Quantitative variable between these groups
- We treat our dataset as a sample from the population, which we cannot access
- We can apply all the CLT ideas +
t.testif the two variables in the dataset satisfy the conditions of normality, equal variance - Else use non-parametric
wilcox.test - And by treating the two variables as one Quant in two groups, we can simply perform a Permutation test
- We have learnt how to perform inference for independent means.
- We have looked at the conditions that make the regular
t.testpossible, and learnt what to do if the conditions of normality and equal variance are not met.
- We have also looked at how these tests can be understood as manifestations of the linear model, with data and sign-ranked data.
Try the
SwimRecordsdataset from themosaicDatapackage.Try some of the datasets in the
moderndivepackage. Install it , peasants. And type in your Consoledata(package = "moderndive")to see what you have. Teacherevalsmight interest you!
- Randall Pruim, Nicholas J. Horton, Daniel T. Kaplan, Start Teaching with R
- https://bcs.wiley.com/he-bcs/Books?action=index&itemId=111941654X&bcsId=11307
- https://statsandr.com/blog/wilcoxon-test-in-r-how-to-compare-2-groups-under-the-non-normality-assumption/
| Package | Version | Citation |
|---|---|---|
| infer | 1.0.9 | @infer |
| openintro | 2.5.0 | @openintro |
| resampledata | 0.3.2 | @resampledata |
| TeachHist | 0.2.1 | @TeachHist |
| TeachingDemos | 2.13 | @TeachingDemos |
| tinytable | 0.13.0 | @tinytable |
| visStatistics | 0.1.7 | @visStatistics |