Testing a Single Proportion

Arvind V.

2022-11-10

Setting up R packages

library(tidyverse)
library(mosaic)
library(ggformula)
library(infer)

## Datasets from Chihara and Hesterberg's book (Second Edition)
library(resampledata)

## Datasets from Cetinkaya-Rundel and Hardin's book (First Edition)
library(openintro)

Plot Fonts and Theme

Code

library(systemfonts)
library(showtext)
## Clean the slate
systemfonts::clear_local_fonts()
systemfonts::clear_registry()
##
showtext_opts(dpi = 96) # set DPI for showtext
sysfonts::font_add(
  family = "Alegreya",
  regular = "../../../../../../fonts/Alegreya-Regular.ttf",
  bold = "../../../../../../fonts/Alegreya-Bold.ttf",
  italic = "../../../../../../fonts/Alegreya-Italic.ttf",
  bolditalic = "../../../../../../fonts/Alegreya-BoldItalic.ttf"
)

sysfonts::font_add(
  family = "Roboto Condensed",
  regular = "../../../../../../fonts/RobotoCondensed-Regular.ttf",
  bold = "../../../../../../fonts/RobotoCondensed-Bold.ttf",
  italic = "../../../../../../fonts/RobotoCondensed-Italic.ttf",
  bolditalic = "../../../../../../fonts/RobotoCondensed-BoldItalic.ttf"
)
showtext_auto(enable = TRUE) # enable showtext
##
theme_custom <- function() {
  theme_bw(base_size = 10) +

    # theme(panel.widths = unit(11, "cm"),
    #       panel.heights = unit(6.79, "cm")) + # Golden Ratio

    theme(
      plot.margin = margin_auto(t = 1, r = 2, b = 1, l = 1, unit = "cm"),
      plot.background = element_rect(
        fill = "bisque",
        colour = "black",
        linewidth = 1
      )
    ) +

    theme_sub_axis(
      title = element_text(
        family = "Roboto Condensed",
        size = 10
      ),
      text = element_text(
        family = "Roboto Condensed",
        size = 8
      )
    ) +

    theme_sub_legend(
      text = element_text(
        family = "Roboto Condensed",
        size = 6
      ),
      title = element_text(
        family = "Alegreya",
        size = 8
      )
    ) +

    theme_sub_plot(
      title = element_text(
        family = "Alegreya",
        size = 14, face = "bold"
      ),
      title.position = "plot",
      subtitle = element_text(
        family = "Alegreya",
        size = 10
      ),
      caption = element_text(
        family = "Alegreya",
        size = 6
      ),
      caption.position = "plot"
    )
}

## Use available fonts in ggplot text geoms too!
ggplot2::update_geom_defaults(geom = "text", new = list(
  family = "Roboto Condensed",
  face = "plain",
  size = 3.5,
  color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "label", new = list(
  family = "Roboto Condensed",
  face = "plain",
  size = 3.5,
  color = "#2b2b2b"
))

ggplot2::update_geom_defaults(geom = "marquee", new = list(
  family = "Roboto Condensed",
  face = "plain",
  size = 3.5,
  color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "text_repel", new = list(
  family = "Roboto Condensed",
  face = "plain",
  size = 3.5,
  color = "#2b2b2b"
))
ggplot2::update_geom_defaults(geom = "label_repel", new = list(
  family = "Roboto Condensed",
  face = "plain",
  size = 3.5,
  color = "#2b2b2b"
))

## Set the theme
ggplot2::theme_set(new = theme_custom())

## tinytable options
options("tinytable_tt_digits" = 2)
options("tinytable_format_num_fmt" = "significant_cell")
options(tinytable_html_mathjax = TRUE)


## Set defaults for flextable
flextable::set_flextable_defaults(font.family = "Roboto Condensed")

Introduction

Often we hear reports that a certain percentage of people support a certain political party, or that a certain proportion of people are in favour of a certain policy. Such statements are the result of a desire to infer a proportion in the population, which is what we will investigate here.

Workflow: Sampling Theory for Proportions

We have seen how sampling from a population works when we wish to estimate means:

The sample means $\bar{x}$ are centred around the population mean $\mu$;
The samples means are normally distributed
The uncertainty in using $\bar{x}$ as an estimate for $\mu$ is given by a Confidence interval defined by some constant times the Standard Error of the sample $\frac{s}{\sqrt(n)}$;
The larger the size of the sample, the tighter the Confidence Interval.

Now then: does a similar logic work for proportions too, as for means?

The CLT for Proportions

The Central Limit Theorem (CLT) also works for proportions, with some differences:

Sample proportions are also centred around population proportions
Success-failure condition: If \[ \hat{p} *n >= 10 \] and \[ (1-\hat{p})*n >= 10 \] are both satisfied, then the we can assume that the sampling distribution of the proportion is normal. And so:
The Standard Error for a sample proportion is given by \[ \Large{SE = \sqrt\frac{\hat{p}(1-\hat{p})}{n}} \tag{1}\] where $\hat{p}$ is the sample proportion.
We would calculate the Confidence Intervals in a similar fashion, based on the desired probability of error, as:

\[ \Large{p = \hat{p} \pm 1.96*{SE}} \tag{2}\]

The larger the size of the sample, the tighter the Confidence Interval.

Case Study #1: YRBSS Survey

We will be analyzing the same dataset called the Youth Risk Behavior Surveillance System (YRBSS) survey from the openintro package, which uses data from high schoolers to help discover health patterns. The dataset is called yrbss.

Workflow: Read the Data

data(yrbss, package = "openintro")
yrbss

When summarizing the YRBSS data, the Centers for Disease Control and Prevention seeks insight into the population parameters. Accordingly, in this tutorial, our research questions are:

Research Questions

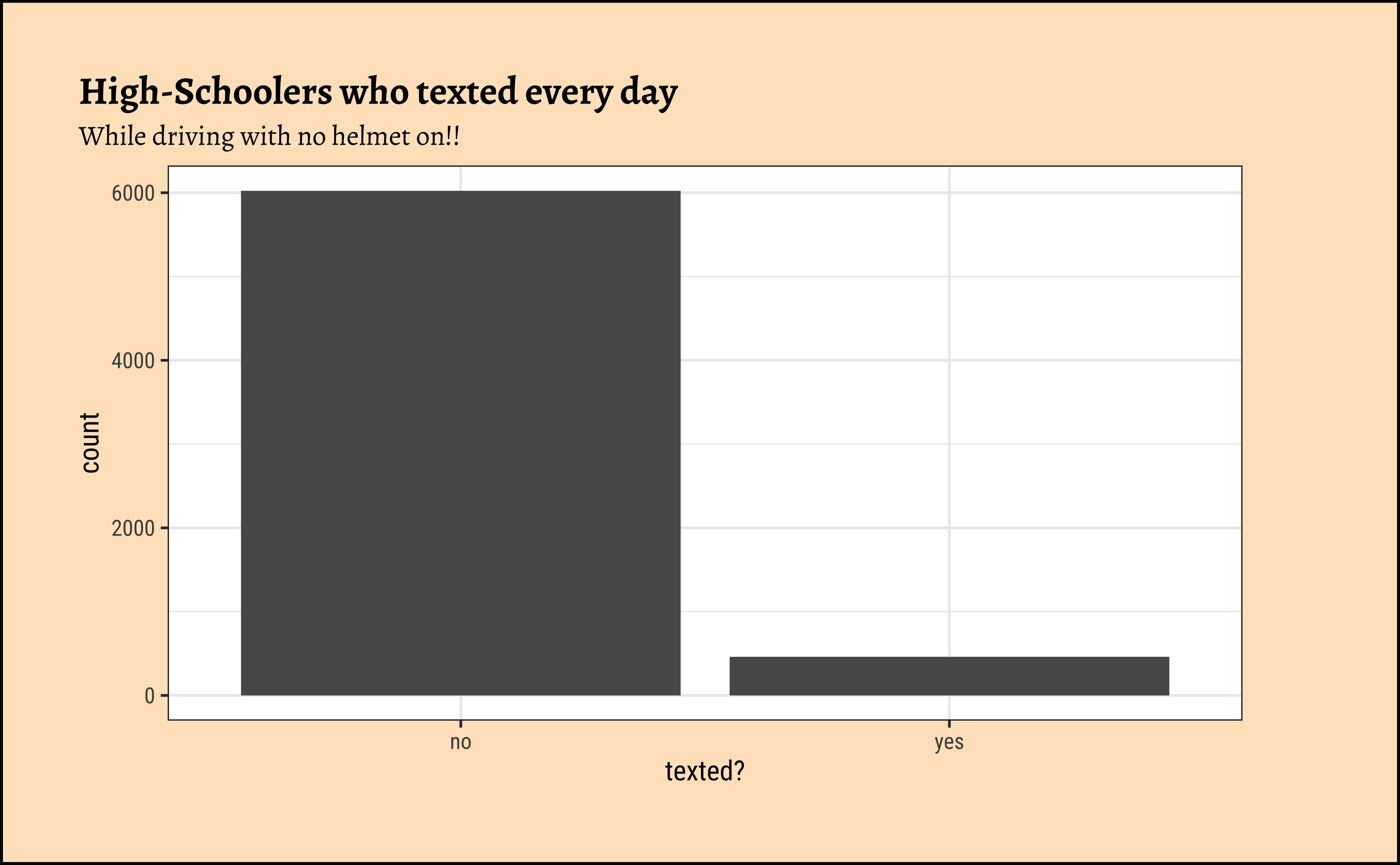
What are the counts within each category for the amount of days these students have texted while driving within the past 30 days?
What proportion of people on earth have texted while driving each day for the past 30 days without wearing helmets?

Question 1 pertains to the data set yrbss, our “sample”. To answer this, you can answer the question, “What proportion of people in your sample reported that they have texted while driving each day for the past 30 days?” with an observed statistic.

Question 2 is an inference we need to make about the population of highschoolers. While the question “What proportion of people on earth have texted while driving each day for the past 30 days?” is answered with an estimate of the parameter.

For our first Research Question, we will choose the column helmet_12m: Remember that you can use filter to limit the dataset to just non-helmet wearers. Here, we will name the (filtered ) dataset no_helmet.

yrbss %>%
  group_by(helmet_12m) %>%
  count()

yrbss %>%
  group_by(text_while_driving_30d) %>%
  count()

Also, it may be easier to calculate the proportion if we create a new variable that specifies whether the individual has texted every day while driving over the past 30 days or not. We will call this variable text_ind.

no_helmet_text <- yrbss %>%
  filter(helmet_12m == "never") %>%
  mutate(text_ind = ifelse(text_while_driving_30d == "30", "yes", "no")) %>%
  # removing most of the other variables
  select(age, gender, text_ind)
no_helmet_text

no_helmet_text %>%
  drop_na() %>%
  count(text_ind)

no_helmet_text %>%
  drop_na() %>%
  summarize(prop = prop(text_ind, success = "yes"), n = n())

This is the observed_statistic: the proportion of people in this sample who do text when they drive without a helmet.

Visualizing a Single Proportion

We can quickly plot this, just for the sake of visual understanding of the proportions:

ggplot2::theme_set(new = theme_custom())

no_helmet_text %>%
  drop_na() %>%
  gf_bar(~text_ind) %>%
  gf_labs(
    x = "texted?",
    title = "High-Schoolers who texted every day",
    subtitle = "While driving with no helmet on!!"
  )

Figure 1: High-Schoolers who texted every day while driving with no helmet on!!

Inference for a Single Proportion

Based on this sample in the yrbss data, we wish to infer proportions for the population of high-schoolers.

Hypothesis Testing for a Single Proportion

Consider the inference we did for a single mean. What was our NULL Hypothesis? That the population mean $\mu = 0$. For two means? That they might be equal. What might a suitable NULL Hypothesis be for a single proportion? What attitude of ain’t nothing happenin’ might we adopt?

Important

With proportions, we usually look for a “no difference” situation, i.e. a ratio of unity!! So our NULL hypothesis would be a ratio of 1:1 for texters and no-texters, so a proportion of $0.5$!!

The simplest test in R for a single proportion is the binom.test:

mosaic::binom.test(~text_ind, data = no_helmet_text, success = "yes")




data:  no_helmet_text$text_ind  [with success = yes]
number of successes = 463, number of trials = 6503, p-value < 2.2e-16
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
 0.06506429 0.07771932
sample estimates:
probability of success 
            0.07119791

mosaic::binom.test(~text_ind, data = no_helmet_text, success = "yes") %>%
  broom::tidy()

How do we understand this result? That the sample tells us the $\hat{p} = 0.07119$ and that based on this the population proportion of those who text while driving without a helmet is also not 0.5, since the p-value is $2.2e-16$. So we reject the NULL hypothesis and accept the alternative hypothesis, that the proportion is not 0.5 and more like 0.07119.

The Confidence Intervals from the binom.test inform us about our population proportion estimate: It lies within the interval [0.06506429, 0.07771932]. We know that this is also given by:

\[ \begin{eqnarray} CI &=& \hat{p} ~ \pm 1.96*SE\\ &=& \hat{p} ~ \pm 1.96*\sqrt{\hat{p}* (1-\hat{p})/n}\\ &=& 0.0711 \pm 1.96*\sqrt{0.0711 * (1- 0.0711)/6847}\\ &=& 0.0711 \pm 0.006\\ &=& [0.065, 0.771] \end{eqnarray} \]

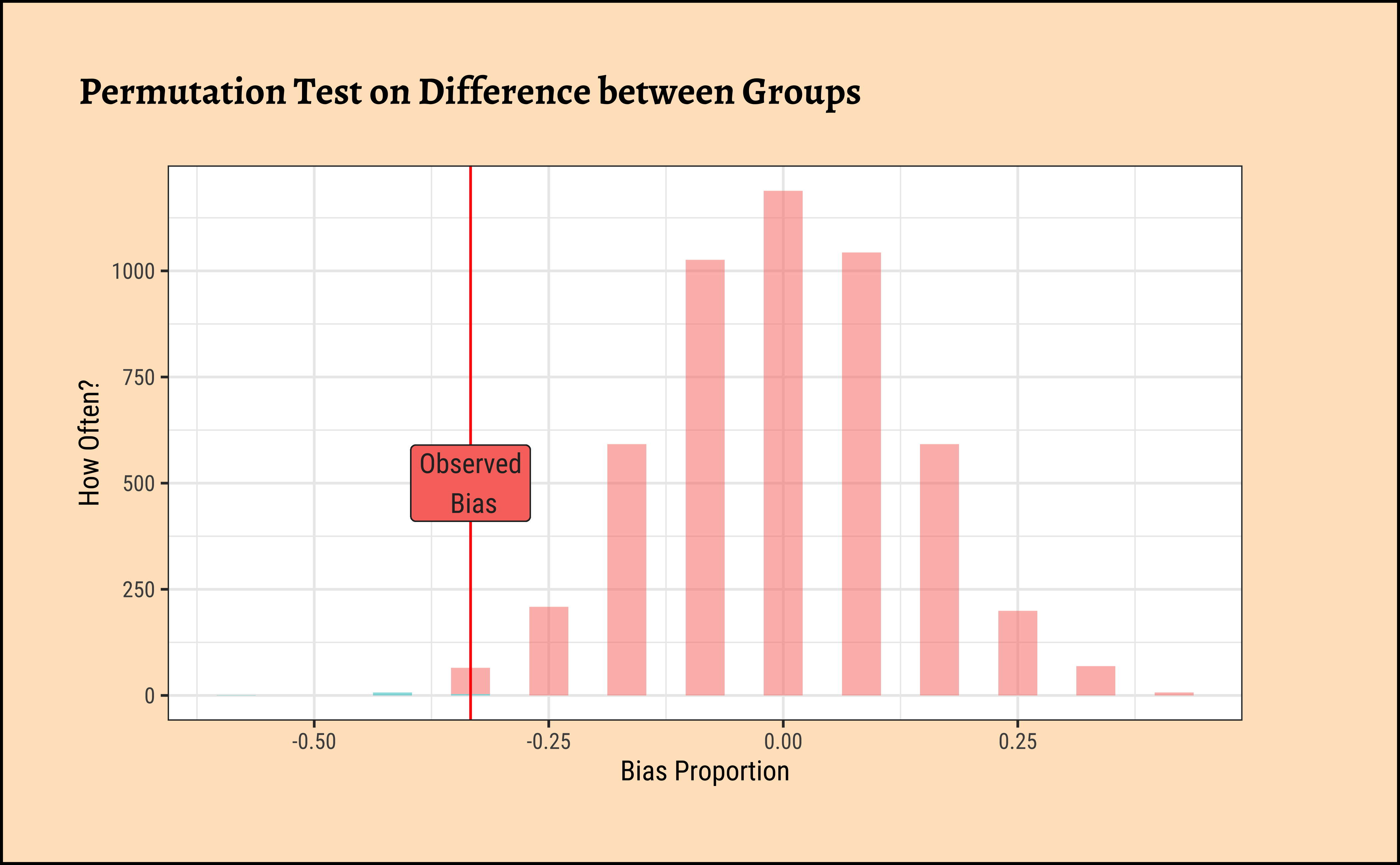
Permutation Visually Demonstrated

We saw from the diagram created by Allen Downey that there is only one test! We will now use this philosophy to develop a technique that allows us to mechanize several Statistical Models in that way, with nearly identical code. We will first look visually at a permutation exercise. We will create dummy data that contains the following case study:

A set of identical resumes was sent to male and female evaluators. The candidates in the resumes were of both genders. We wish to see if there was difference in the way resumes were evaluated, by male and female evaluators. (We use just one male and one female evaluator here, to keep things simple!)

         M 
-0.3333333

So, we have a solid disparity in percentage of selection between the two evaluators! Now we pretend that there is no difference between the selections made by either set of evaluators. So we can just:

Pool up all the evaluations
Arbitrarily re-assign a given candidate(selected or rejected) to either of the two sets of evaluators, by permutation.

How would that pooled shuffled set of evaluations look like?

As can be seen, the ratio is different!

We can now check out our Hypothesis that there is no bias. We can shuffle the data many many times, calculating the ratio each time, and plot the distribution of the differences in selection ratio and see how that artificially created distribution compares with the originally observed figure from Mother Nature.

ggplot2::theme_set(new = theme_custom())

null_dist <- do(4999) * diff(mean(
  candidate_selected ~ shuffle(evaluator),
  data = data
))
# null_dist %>% names()
null_dist %>%
  gf_histogram(~M,
    fill = ~ (M <= obs_difference),
    bins = 25, show.legend = FALSE,
    xlab = "Bias Proportion",
    ylab = "How Often?",
    title = "Permutation Test on Difference between Groups",
    subtitle = ""
  ) %>%
  gf_vline(xintercept = ~obs_difference, color = "red") %>%
  gf_label(500 ~ obs_difference,
    label = "Observed\n Bias",
    show.legend = FALSE
  )
mean(~ M <= obs_difference, data = null_dist)

[1] 0.00220044

We see that the artificial data can hardly ever ($p = 0.0022$) mimic what the real world experiment is showing. Hence we had good reason to reject our NULL Hypothesis that there is no bias.

The inferential tools for estimating a single population proportion are analogous to those used for estimating single population means: the bootstrap confidence interval and the hypothesis test.

no_helmet_text %>%
  drop_na() %>%
  specify(response = text_ind, success = "yes") %>%
  generate(reps = 999, type = "bootstrap") %>%
  calculate(stat = "prop") %>%
  get_ci(level = 0.95)

Note that since the goal is to construct an interval estimate for a proportion, it’s necessary to both include the success argument within specify, which accounts for the proportion of non-helmet wearers than have consistently texted while driving the past 30 days, in this example, and that stat within calculate is here “prop”, signaling that we are trying to do some sort of inference on a proportion.

Case Study #2: TBD

To be Written up in the foreseeable future. Yeah. Never Mind.

An interactive app

https://openintro.shinyapps.io/CLT_prop/

Wait, But Why?

In business, or “design research”, one encounters things that are proportions in a target population:
- Adoption of a service or an app
- People preferring a particular product
- Beliefs which are of Yes/No type: Is this Govt. doing the right thing with respect to taxes?
- Knowing what this population proportion is a necessary step to take a decision about what you will do about it.
- (Other than plot a *&^%#$$%^& pie chart)

Conclusion

We have seen how the CLT works with proportions, in a manner similar to that with means
The Standard Error (and therefore the CI) for the inference of a proportion is related to the actual population proportion, which is very different behaviour from that with means, where SE was just a number that depended on the sample size
Bootstrap procedures work with inference for a single proportion. (Permutation when there are two)

Your Turn

Type data(package = "resampledata") and data(package = "resampledata3") in your RStudio console. This will list the datasets in both these package. Try loading a few of these and infering for single proportions.
National Health and Nutrition Examination Survey (NHANES) dataset. Install the package NHANES and explore the dataset for proportions that might be interesting.

References

StackExchange. prop.test vs binom.test in R. https://stats.stackexchange.com/q/551329
Mine Çetinkaya-Rundel and Johanna Hardin, OpenIntro Modern Statistics: Chapter 17
Laura M. Chihara, Tim C. Hesterberg, Mathematical Statistics with Resampling and R. 3 August 2018.© 2019 John Wiley & Sons, Inc.
OpenIntro Statistics Github Repo: https://github.com/OpenIntroStat/openintro-statistics

R Package Citations

Package	Version	Citation
ggbrace	0.1.2	Huber (2025)
openintro	2.5.0	Çetinkaya-Rundel et al. (2024)
resampledata	0.3.2	Chihara and Hesterberg (2018)

Çetinkaya-Rundel, Mine, David Diez, Andrew Bray, Albert Y. Kim, Ben Baumer, Chester Ismay, Nick Paterno, and Christopher Barr. 2024. openintro: Datasets and Supplemental Functions from “OpenIntro” Textbooks and Labs. https://doi.org/10.32614/CRAN.package.openintro.

Chihara, Laura M., and Tim C. Hesterberg. 2018. Mathematical Statistics with Resampling and r. John Wiley & Sons Hoboken NJ. https://github.com/lchihara/MathStatsResamplingR?tab=readme-ov-file.

Huber, Nicolas. 2025. ggbrace: Curly Braces for “ggplot2”. https://doi.org/10.32614/CRAN.package.ggbrace.